











На протяжении всей этой
главы мы будем рассматривать ограниченные линейные операторы, отображающие
некоторое (вообще говоря комплексное) банахово пространство Е в себя.
Оператор, сопряженный оператору указанного типа; будет, очевидно, отображать
сопряженное пространство ![]() в себя.
в себя.
При изучении линейных операторов в конечномерном пространстве важную роль играют понятия собственного вектора и собственного значения. В случае n-мерного пространства понятие собственного значения оператора можно ввести следующими, эквивалентными между собой, способами:
1) Число ![]() называется собственным значением оператора
А, если существует такой ненулевой вектор х (собственный вектор),
что
называется собственным значением оператора
А, если существует такой ненулевой вектор х (собственный вектор),
что
![]()
2) Число ![]() называется собственным значением оператора
А, если оно является корнем характеристического уравнения
называется собственным значением оператора
А, если оно является корнем характеристического уравнения
![]()
Первое из этих определений переносится без всяких изменений на случай бесконечномерного пространства, т. е. его можно рассматривать как определение собственных значений оператора в бесконечномерном пространстве.
Второе из
сформулированных определений непосредственно на бесконечномерный случай не переносится,
так как в бесконечномерном пространстве понятие определителя не имеет смысла.
Однако это второе определение можно видоизменить следующим образом. Обращение в
нуль определителя матрицы ![]() равносильно
необратимости этой матрицы, т. е. можно сказать, что собственные значения
равносильно
необратимости этой матрицы, т. е. можно сказать, что собственные значения ![]() суть те числа, для которых оператор
суть те числа, для которых оператор ![]() необратим. Исходя из этого, введем
следующее определение:
необратим. Исходя из этого, введем
следующее определение:
Совокупность тех
значений ![]() для которых оператор
для которых оператор ![]() необратим, называется спектром оператора
А. Значения А, при которых оператор
необратим, называется спектром оператора
А. Значения А, при которых оператор ![]() обратим,
называются регулярными, таким образом, спектр состоит из всех
нерегулярных точек. При этом сам оператор
обратим,
называются регулярными, таким образом, спектр состоит из всех
нерегулярных точек. При этом сам оператор ![]() называется
резольвентой оператора А. В n-мерном пространстве понятия
собственного значения и нерегулярной точки совпадают. В общем случае, как показывает
приводимый ниже пример, это не так. Спектр обязательно содержит все собственные
значения, но может содержать, кроме них, и другие числа. Совокупность собственных
значений называется точечным спектром оператора А. Остальная
часть спектра носит название непрерывного спектра.
называется
резольвентой оператора А. В n-мерном пространстве понятия
собственного значения и нерегулярной точки совпадают. В общем случае, как показывает
приводимый ниже пример, это не так. Спектр обязательно содержит все собственные
значения, но может содержать, кроме них, и другие числа. Совокупность собственных
значений называется точечным спектром оператора А. Остальная
часть спектра носит название непрерывного спектра.
Если точка ![]() регулярна, т.
е. оператор
регулярна, т.
е. оператор ![]() обратим, то при достаточно малом
обратим, то при достаточно малом ![]() оператор
оператор ![]() также
обратим (теорема 7 § 29), т. е. точка
также
обратим (теорема 7 § 29), т. е. точка ![]() также
регулярна. Таким образом, регулярные точки образуют открытое множество. Следовательно,
спектр — его дополнение — замкнутое множество.
также
регулярна. Таким образом, регулярные точки образуют открытое множество. Следовательно,
спектр — его дополнение — замкнутое множество.
Теорема 1.
Оператор ![]() обратим
при любом
обратим
при любом ![]() таком, что
таком, что ![]()
Доказательство. Так как, очевидно,
![]()
то
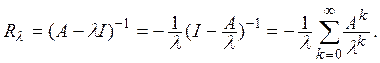
При ![]() этот
ряд сходится (см. теорему 8 §29), т.е. оператор
этот
ряд сходится (см. теорему 8 §29), т.е. оператор ![]() обратим.
Иначе говоря, спектр оператора А помещается в круге радиуса
обратим.
Иначе говоря, спектр оператора А помещается в круге радиуса ![]() с центром в нуле.
с центром в нуле.
Пример. В пространстве С рассмотрим оператор А, определяемый формулой
![]()
где ![]() — фиксированная
непрерывная функция. Имеем
— фиксированная
непрерывная функция. Имеем
![]()
откуда
![]()
Спектр рассматриваемого оператора А состоит
из всех ![]() для которых
для которых ![]() обращается
в нуль, при некотором t, заключенном между 0
и 1, т.е. спектр есть совокупность всех значений функции
обращается
в нуль, при некотором t, заключенном между 0
и 1, т.е. спектр есть совокупность всех значений функции ![]() Например, если
Например, если ![]() то
спектр представляет собой отрезок
то
спектр представляет собой отрезок ![]() причем собственные
значения отсутствуют, т. е. оператор умножения на t представляет собой пример оператора с чисто непрерывным
спектром.
причем собственные
значения отсутствуют, т. е. оператор умножения на t представляет собой пример оператора с чисто непрерывным
спектром.
(1) Всякий линейный оператор, определенный в банаховом пространстве, имеющем хотя бы один отличный от нуля элемент, имеет не пустой спектр. Существуют операторы, у которых спектр состоит из единственной точки (например, оператор умножения на число).
(2) Теорема 1 может быть уточнена следующим образом. Пусть
![]()
тогда спектр оператора А целиком лежит внутри круга радиуса r с центром в нуле.
(3)
Резольвентные операторы ![]() и
и ![]() отвечающие точкам
отвечающие точкам ![]() и
и
![]() перестановочны между собой и удовлетворяют
соотношению
перестановочны между собой и удовлетворяют
соотношению
![]()
которое легко проверить, умножив обе части этого равенства на
![]()
Отсюда вытекает, что производная от ![]() по
по ![]() т. е.
т. е.
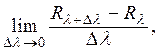
существует и равна ![]()
Определение. Оператор А, отображающий банахово пространство Е в себя, называется вполне непрерывным, если он переводит любое ограниченное множество в компактное.
В конечномерном пространстве всякий ограниченный линейный оператор вполне непрерывен, так как он переводит любое ограниченное множество снова в ограниченное, а в конечномерном пространстве всякое ограниченное множество компактно.
В случае бесконечномерного пространства всегда существуют операторы, ограниченные (т. е. непрерывные), но не вполне непрерывные; таким, например, будет единичный оператор в бесконечномерном пространстве.
В пространстве ![]() обширный класс вполне непрерывных
операторов
обширный класс вполне непрерывных
операторов
![]()
может быть записан в виде
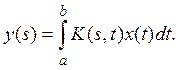 (1)
(1)
Теорема 1.
Формула (1) определяет вполне непрерывный оператор в пространстве
![]() если функция K(s, t) ограничена
на квадрате
если функция K(s, t) ограничена
на квадрате ![]() все точки разрыва функции K(s, t) лежат
на конечном числе кривых
все точки разрыва функции K(s, t) лежат
на конечном числе кривых
![]()
где ![]() —
непрерывные функции[1].
—
непрерывные функции[1].
Доказательство. Заметим, что
при условиях теоремы интеграл (1) существует для любого s
из отрезка ![]() Пусть
Пусть ![]() на квадрате
на квадрате ![]() Обозначим
через G множество
точек (s, t), для которых при
каких-либо k = 1, 2, ..., n выполняется неравенство:
Обозначим
через G множество
точек (s, t), для которых при
каких-либо k = 1, 2, ..., n выполняется неравенство:
![]()
и через F — дополнение к G до полного
квадрата ![]() Так как F замкнуто, и K(s, t) непрерывно на F, то существует такое
Так как F замкнуто, и K(s, t) непрерывно на F, то существует такое ![]() что для
точек (s', t), (s", t) из F с
что для
точек (s', t), (s", t) из F с ![]() будет выполнено неравенство
будет выполнено неравенство
![]()
Пусть теперь s' и s" таковы, что ![]() Тогда
Тогда

может быть подсчитан при помощи интегрирования по сумме интервалов
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.