Линейные операторные уравнения, страница 3

Теорема 5. Всякий вполне непрерывный оператор А в банаховом пространстве Е имеет при любом  только конечное число линейно независимых собственных векторов, отвечающих собственным значениям, по модулю превосходящим

Доказательство. 1°. Заметим прежде всего, что каждое отличное от нуля собственное значение вполне непрерывного оператора имеет конечную кратность. Действительно, совокупность  всех собственных векторов, отвечающих данному собственному значению  представляет собой линейное подпространство, размерность которого равна кратности этого собственного значения. Если бы для некоторого  это подпространство было бесконечномерно, то оператор А не был бы вполне непрерывен в  а следовательно, и во всем пространстве.

2°. Теперь для завершения доказательства теоремы остается показать, что какова бы ни была последовательность  попарно различных собственных значений вполне непрерывного оператора  при  Пусть  — собственный вектор оператора А, отвечающий собственному значению  Векторы  линейно независимы. Пусть   — подпространство, состоящее из всех элементов вида 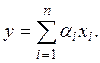 Для каждого  имеем:

откуда видно, что

Выберем последовательность элементов  так, что

(Возможность выбора такой последовательности показана в примечании на стр. 116)

Предположим теперь, что последовательность  ограничена. Тогда множество 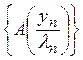 должно быть компактно, но это невозможно, так как при

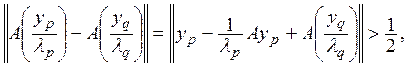
поскольку 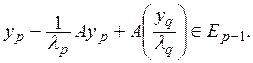 Полученное противоречие доказывает наше утверждение.

Из этой теоремы вытекает, что каждое отличное от нуля собственное значение вполне непрерывного оператора имеет лишь конечную кратность, и эти собственные значения образуют ограниченное множество, которое не может иметь ни одной предельной точки, отличной от начала координат. Мы получили, таким образом, характеристику точечного спектра вполне непрерывного оператора. Из результатов следующего параграфа будет вытекать, что непрерывного спектра вполне непрерывный оператор иметь не может.

§ 32. Линейные операторные уравнения. Теоремы Фредгольма

В этом параграфе мы будем рассматривать уравнения вида

                                                              (1)

где А — вполне непрерывный оператор, отображающий банахово пространство Е в себя. Мы покажем, что для таких уравнений справедлив ряд теорем, аналогичных теоремам, известным для систем линейных алгебраических уравнений. Первоначально соответствующая теория была развита Фредгольмом для интегральных уравнений вида

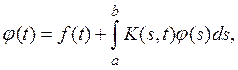
где f(t) и K(s, t) — заданные непрерывные функции.

В предыдущем параграфе было установлено, что оператор Фредгольма

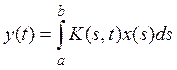
вполне непрерывен; таким образом, уравнение (1) действительно является обобщением интегрального уравнения Фредгольма (2).

Теорема 1. Пусть А — вполне непрерывный оператор, отображающий банахово пространство Е в себя. Если уравнение

разрешимо при любом у, то уравнение

не имеет никаких решений, отличных от нулевого.

Доказательство. Предположим противное: пусть существует такой элемент  что

Те элементы х, для которых Тх = 0, образуют линейное подпространство  пространства Е. Подпространство, состоящее из элементов, удовлетворяющих условию

обозначим

Ясно, что подпространства  образуют неубывающую подпоследовательность:

Покажем, что на самом деле равенства здесь ни на каком месте быть не может. Действительно, так как по условию  и уравнение  разрешимо при любом у, то найдется такая последовательность отличных от нуля элементов  что

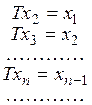
При каждом п элемент  принадлежит подпространству  но не принадлежит подпространству  В самом деле,

но

Все подпространства  линейны и замкнуты, поэтому для любого п существует такой элемент  что[2]

где  означает расстояние от  до подпространства  т. е.

Рассмотрим последовательность  Имеем (полагая ):

так как  Отсюда видно, что последовательность  не может содержать никакой сходящейся подпоследовательности, что противоречит полной непрерывности оператора А. Полученное противоречие доказывает теорему.

Следствие 1. Если уравнение  разрешимо при любом у, то оно при каждом у имеет единственное решение, т. е. в этом случае оператор  обратим.