Линейные операторные уравнения, страница 4

Действительно, если бы уравнение  при некотором у имело два различных решения, скажем,  и  то уравнение  имело бы ненулевое решение  что противоречит теореме 1.

Для дальнейшего удобно рассматривать наряду с уравнением  сопряженное ему уравнение  где А* — оператор, сопряженный к A, a h, f — элементы банахова пространства  сопряженного к Е.

Для сопряженного уравнения мы можем сформулировать следующий результат:

Следствие 2. Если уравнение  разрешимо при всех h, то уравнение  имеет только нулевое решение.

Это утверждение получается из теоремы 1, если принять во внимание, что оператор, сопряженный к вполне непрерывному, вполне непрерывен (теорема 2 §31), а пространство, сопряженное с банаховым, само есть банахово пространство.

Теорема 2. Для того чтобы уравнение

было разрешимо, необходимо и достаточно, чтобы выполнялось условие: f(y) = 0 для всех f таких, что

Доказательство. 1. Пусть уравнение  разрешимо, тогда

т.е. f(y) = 0 для всех f, удовлетворяющих уравнению

2. Пусть теперь f(у) равно нулю для всех f, удовлетворяющих уравнению  Для каждого из этих функционалов f рассмотрим множество  элементов, на которых f обращается в нуль. Тогда наше утверждение равносильно тому, что множество  состоит только из элементов вида  т. е. нам нужно доказать, что элемент  не представимый в виде  не может входить в  Для этого мы покажем, что для такого элемента  можно построить функционал  удовлетворяющий условиям

Эти условия равносильны следующим:

Действительно,

Пусть  — линейное многообразие, состоящее из всех элементов вида  Покажем, что  замкнуто. Пусть  есть взаимно однозначное отображение фактор-пространства  (где N — подпространство элементов, удовлетворяющих условию ) на  Нужно показать, что обратное отображение  непрерывно. Достаточно доказать непрерывность его в точке у = 0. 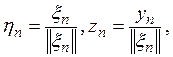Предположим, что это не так; тогда существует последовательность  такая, что для  выполнено неравенство  Положив,  получаем последовательность  удовлетворяющую условиям:  Выбрав в каждом классе  по представителю  так, что  получим ограниченную последовательность, удовлетворяющую условию:  Но так как оператор А вполне непрерывен,  содержит фундаментальную последовательность  последовательность  тоже фундаментальна и потому сходится к некоторому элементу  Поэтому  откуда  т.е.  Но тогда  что противоречит условию  Полученное противоречие доказывает непрерывность отображения  а следовательно, и замкнутость  Таким образом,  есть подпространство. Рассмотрим подпространство  т. е. совокупность элементов вида

и определим линейный функционал  на этом подпространстве, положив

Продолжив этот функционал на все пространство Е (что возможно в силу теоремы Хана-Банаха), мы и получим линейный функционал, удовлетворяющий поставленным условиям. Теорема доказана.

Следствие. Если уравнение  не имеет ненулевых решений, то уравнения  разрешимо при всех у.

Установим теорему, аналогичную теореме 2, для сопряженного уравнения.

Теорема 3. Для того чтобы уравнение

было разрешимо, необходимо и достаточно, чтобы выполнялось условие h(x) = 0 для всех х таких, что

Доказательство. 1. Пусть уравнение  разрешимо, тогда

т. e. h(x) = 0, если

2. Пусть теперь  для всех х, удовлетворяющих уравнению  Покажем, что уравнение (1) разрешимо. Построим на множестве F всех элементов вида  функционал f, положив

                                                             (4)

Это равенство действительно определяет линейный функционал. Прежде всего заметим, что для каждого у значение функционала f определяется однозначно, так как если  то  Линейность функционала (4) легко проверяется. Этот функционал f можно продолжить на все пространство Е. Получаем:

т. е. этот функционал f служит решением уравнения (3).

Следствие. Если уравнение  не имеет ненулевых решений, то уравнение  разрешимо при всех h. Следующая теорема является обратной к теореме 1.

Теорема 4. Если уравнение  имеет единственное решение (х = 0), то уравнение  имеет решение при всех у.

Доказательство. Если уравнение  имеет единственное решение, то в силу следствия из предыдущей теоремы уравнение  разрешимо для всех h. Тогда, по теореме 1, уравнение  имеет только нулевое решение, откуда, согласно следствию из теоремы 2, вытекает разрешимость уравнения: