Линейные операторные уравнения, страница 2

(обозначим эту сумму А) и по дополнению В к А до отрезка [а, b]. Длина А не превосходит  Поэтому,

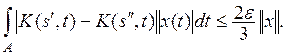
Интеграл до В, очевидно, допускает оценку

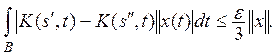
Поэтому

Мы доказали непрерывность y(s) и равностепенную непрерывность функций y(s), соответствующих функциям x(t) с ограниченной нормой. Равномерная ограниченность y(s), соответствующих x(t) с ограниченной нормой, вытекает из неравенства

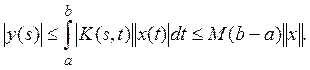
Оператор Вольтерра. Если считать, что  при t > s, то оператор (1) принимает вид

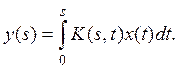                                                      (2)

При  функцию K(s, t) будем предполагать непрерывной. Для такого ядра справедливость условий теоремы 1 легко проверить. Следовательно, этот оператор вполне непрерывен.

Установим некоторые свойства вполне непрерывных операторов.

Теорема 2. Если  — последовательность вполне непрерывных операторов в банаховом пространстве Е, сходящаяся по норме к некоторому оператору А, то оператор А тоже вполне непрерывен.

Доказательство. Рассмотрим некоторую ограниченную последовательность элементов  из Е;  Нужно доказать, что из последовательности  можно выделить сходящуюся подпоследовательность.

Оператор  вполне непрерывен, поэтому из последовательности  можно выбрать сходящуюся подпоследовательность. Пусть

                                                         (3)

прообразы членов этой сходящейся подпоследовательности. Ко всем членам подпоследовательности (3) применим оператор  Так как он вполне непрерывен, то из последовательности  опять-таки можно выделить сходящуюся подпоследовательность, прообразы членов которой пусть будут

К этой последовательности  применим оператор  затем аналогичным образом выберем подпоследовательность  и т. д.

Образуем диагональную последовательность

Каждый из операторов  переводит эту последовательность в сходящуюся. Если мы покажем, что оператор А также переводит эту последовательность в сходящуюся, то полная непрерывность оператора А будет тем самым установлена. Оценим норму разности

Выберем k так, чтобы было  а N выберем так, чтобы для любых  и  выполнялось соотношение

(Это возможно, так как последовательность  сходится.) При этом мы получаем, что  т.е. последовательность  — фундаментальная.

Так как пространство Е полно, то эта последовательность сходится, что и доказывает теорему.

Теорема 3. Оператор, сопряженный с вполне непрерывным, также вполне непрерывен.

Доказательство. Пусть оператор А отображает банахово пространство Е в себя. Тогда сопряженный с ним оператор А* отображает пространство  в себя. Поскольку любое ограниченное множество можно заключить в сферу, теорема будет доказана, если доказать, что образ сферы  принадлежащей пространству  (т.е. множество ), компактен. Достаточно, очевидно, провести доказательство для случая единичной сферы.

Введем в пространстве  вспомогательную метрику, положив для любых двух функционалов  из

                                              (4)

Так как оператор А по предположению вполне непрерывен, то образ AS единичной сферы S в пространстве Е компактен. Если  то  и, следовательно, если  то  т.е.  равномерно ограничены в смысле метрики (4). Далее имеем:

т.е. функционалы  равностепенно непрерывны. Согласно теореме § 17, это означает, что множество  компактно в смысле метрики (4). Но так как

то из компактности множества  в смысле метрики (4) следует компактность множества  в смысле первоначальной метрики пространства

Теорема 4. Если А — вполне непрерывный оператор, а В — ограниченный, то операторы АВ и ВА также вполне непрерывны.

Доказательство. Если М — некоторое ограниченное множество в Е, то множество ВM также ограничено. Следовательно, множество АВМ компактно, а это и означает, что оператор АВ вполне непрерывен. Далее, если М ограничено, то AM компактно, но тогда в силу непрерывности В множество ВАМ также компактно. Теорема доказана.

Следствие. В бесконечномерном пространстве Е вполне непрерывный оператор А не может иметь ограниченного обратного.

Действительно, в противном случае единичный оператор  в Е был бы вполне непрерывен, что невозможно.

Исследуем теперь спектр вполне непрерывного оператора.