Линейные операторные уравнения, страница 5

при любом у.

Теоремы 1 и 4 показывают, что для уравнения

возможны лишь следующие два случая:

1) уравнение (1) имеет единственное решение при каждом у, т.е. оператор  обратим.

2) уравнение  имеет ненулевое решение, т. е. число  является для оператора А собственным значением. Ясно, что все результаты, полученные выше для уравнения  автоматически переносятся и на уравнение

где  — любое число[3]. Мы получаем, что или оператор

обратим, или число  является собственным значением оператора А. Иначе говоря, любое число является для вполне непрерывного оператора или регулярной точкой, или собственным значением, т. е. вполне непрерывный оператор не может иметь непрерывного спектра. Точечный спектр вполне непрерывного оператора был изучен в предыдущем параграфе (теорема 4).

Теорема 5. Размерность п подпространства N, состоящего из решений уравнения  равна размерности  подпространства N* решений уравнения

Доказательство. Заметим прежде всего, что в силу полной непрерывности операторов А и А* подпространства N и N* конечномерны. Пусть  — базис подпространства N, a  - базис подпространства N*. Согласно теореме Хана-Банаха о продолжении линейного функционала, можно построить п функционалов  удовлетворяющих условиям

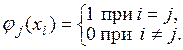
Рассмотрим теперь функционалы  и построим для каждого из них соответствующее подпространство  определяемое условием  Так как функционалы  линейно независимы, то соответствующие множества  попарно различны, а так как каждое из подпространств  имеет индекс 1, то соотношение вида

также невозможно.

Рассмотрим множества

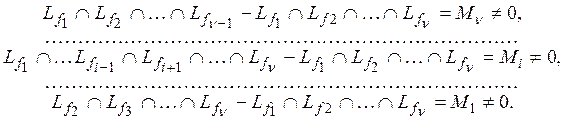
Каждое множество  состоит из тех элементов, которые принадлежат всем  кроме одного. Ясно, что множества  попарно не пересекаются. Так как на каждом  все функционалы  кроме  обращаются в нуль и так как  — линейное многообразие, то можно в каждом  выбрать по точке  так, чтобы выполнялись условия:

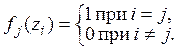                                                       (5)

После этих вспомогательных построений перейдем непосредственно к доказательству утверждения теоремы.

Предположим сперва, что

Построим оператор

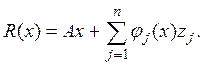
Этот оператор вполне непрерывен, как сумма конечного числа вполне непрерывных операторов. Далее, рассмотрим оператор

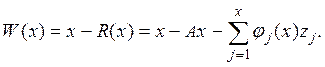
Покажем, что если  то

Применим к  функционал

                      (6)

Так как, по условию,  удовлетворяет уравнению  то  для всех  Кроме того,  так как, по предположению,  Поэтому из (6) вытекает, что

                                               (7)

Но тогда из равенства  следует, что  т. е.  так как элементы  образуют базис в N, то

Применив к этому равенству функционал  и воспользовавшись равенствами (7), получаем, что  Отсюда и из (7) вытекает, что  Мы показали, что уравнение  имеет только нулевое решение. Отсюда следует (теорема 4), что уравнение  разрешимо при всех у, например, при

Пусть х есть решение уравнения  Тогда, с одной стороны, из того, что  и из (5) следует, что

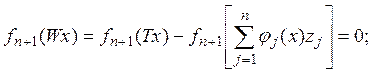
с другой стороны, согласно (5),

Полученное противоречие доказывает, что

Предположим теперь, что  Построим оператор  положив

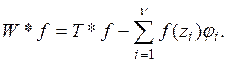                                               (8)

Докажем, что если  то f = 0. Для всех f имеем:

так как  Поэтому, если  то, применив обе части равенства (8) к  получим:

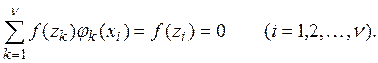                                  (9)

Таким образом, равенство  сводится к  т. е.  Следовательно, f можно записать в виде

Применив обе части этого равенства к элементу  получим, что  Отсюда и из (9) следует, что f = 0. Отсюда вытекает разрешимость уравнения  при всех g.

Пусть f таково, что  Тогда, с одной стороны,

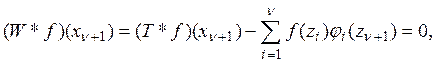
а с другой стороны,

Мы получили противоречие, которое доказывает, что  Итак, окончательно,  Теорема доказана.