Численное интегрирование. Постановка задачи численного интегрирования

6. Численное интегрирование

6.1. Постановка задачи численного интегрирования

Пусть на отрезке  задана сетка , в узлах которых заданы значения , где . Требуется найти число  такое, что

.

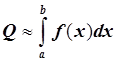Отметим, что задача численного интегрирования является корректно поставленной. Возможны два случая:

1) формула функции  задана, и по этой формуле находятся ;

2) формула функции  не задана, известна только интерполяционная таблица.

Как известно, число 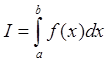    для положительных  равно площади криволинейной трапеции, ограниченной кривой , осью абсцисс и прямыми:  и  (рис. 6.1).

Основная идея численного интегрирования заключается в следующем: вместо площади криволинейной трапеции I будем считать площадь другой фигуры Q, причем должны выполняться два условия:

1) площадь новой фигуры Q должна быть близка к площади криволинейной трапеции;

2) площадь новой фигуры Q должна вычисляться достаточно просто.

Площадь каких геометрических фигур вычисляется очень легко? Площадь прямоугольника  и площадь трапеции. Но, если отрезок  достаточно большой, то площадь прямоугольника или площадь трапеции будут плохо приближать площадь исходной криволинейной трапеции. Чтобы избежать этого, представим  интеграл I в виде суммы:

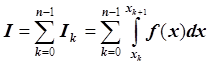
и будем приближать каждый интеграл 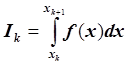  числом  , а интеграл I числом .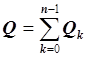

Таким образом, исходная криволинейная трапеция разбивается на n криволинейных трапеций, а вместо площади каждой «маленькой» криволинейной трапеции считается площадь простой фигуры, например, площадь прямоугольника или трапеции.

Рекомендуемая литература: /1-4, 6, 12, 13/.

6.2. Квадратурные формулы

Введем несколько определений.

Определение. Квадратурной формулой называется всякая простая  формула, аппроксимирующая отдельный интеграл :

,            .

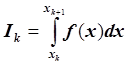Таким образом, любая формула для нахождения  – это квадратурная формула.

Определение. Составная квадратурная формула – это формула, дающая приближение к интегралу

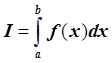
в виде суммы приближений по данной квадратурной формуле к отдельным интегралам :

,             .

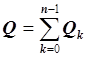Часто вместо «составная квадратурная» формула говорят просто: «формула».

Рассмотрим две простейшие квадратурные формулы: трапеций и прямоугольников.

Квадратурная формула трапеций

Квадратурная формула трапеций аппроксимирует интеграл: .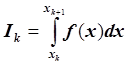

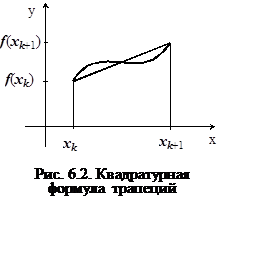
Заменяем площадь «маленькой» криволинейной трапеции площадью обычной трапеции (рис. 6.2).

Квадратурная формула трапеций:

,        .

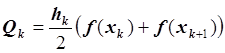,      где     – погрешность квадратурной формулы.

Пояснение. Если   для  , то ,  где с – константа.

Составная квадратурная формула трапеций

Будем считать, что сетка задана с постоянным шагом  .

Запишем интеграл в виде:

,                где     ,               .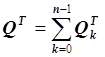

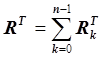Здесь – составная квадратурная формула трапеций:

,           ;

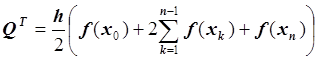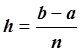 – остаточный член или погрешность формулы трапеций:

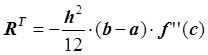,       где  с – некоторая точка из ;

.

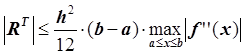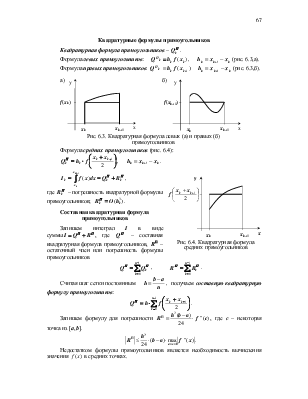
Квадратурные формулы прямоугольников

Квадратурная формула прямоугольников – .

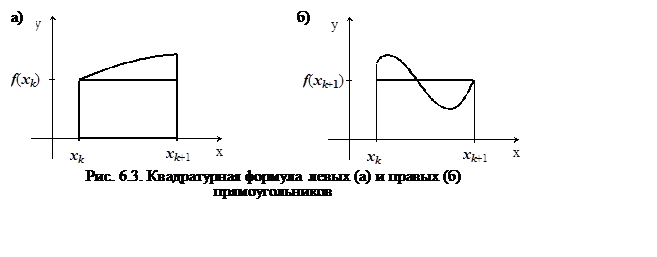
Формула левых прямоугольников:    ,      (рис. 6.3,а).

Формула правых прямоугольников:      (рис. 6.3,б).

,     .

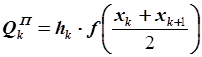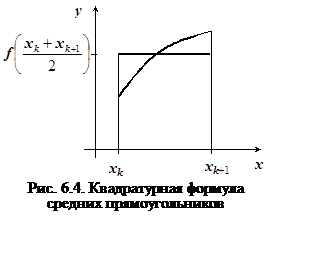
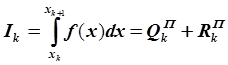, где  – погрешность квадратурной формулы прямоугольников;  .

Составная квадратурная формула            прямоугольников

Запишем интеграл I в виде суммы, где  – составная квадратурная формула прямоугольников,  – остаточный член или погрешность формулы прямоугольников

,            .

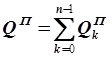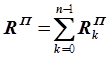Считая шаг сетки постоянным 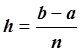   ,  получаем составную квадратурную формулу прямоугольников:

.

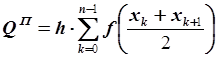Запишем формулу для погрешности 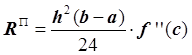, где с – некоторая точка из .

.

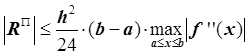Недостатком формулы прямоугольников является необходимость вычисления значения  в средних точках.

6.3. Квадратурная формула Симпсона

Рассмотрим три точки  . По интерполяционной таблице

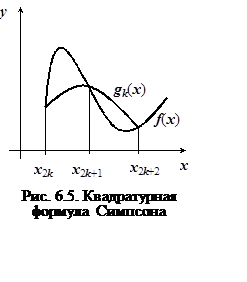мы можем построить единственный интерполяционный полином второй степени (рис.6.5), , а затем вычислить интеграл:    .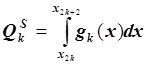

Получим:  – квадратурную формулу Симпсона (рис. 6.5).

Обозначим:  – погрешность квадратурной формулы Симпсона.

Запишем: ,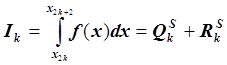

Квадратурная формула Симпсона:

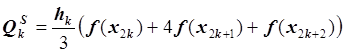, где ;  .

6.4. Составная квадратурная формула Симпсона

Рассмотрим равномерный шаг 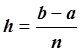 ,        где  .

Запишем интеграл в виде:

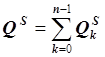,                 где              и        .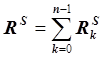

Здесь    – составная квадратурная формула Симпсона:

.

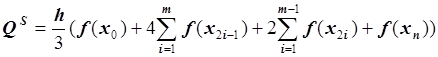Составную квадратурную формулу Симпсона можно использовать, если число интервалов является четным числом, иначе придется вычислять значения в средних точках  .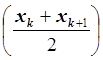

Запишем  – остаточный член или погрешность формулы Симпсона:

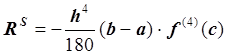,    где с – некоторая точка из ,

.

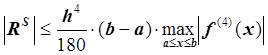Отметим, что удвоение числа элементарных отрезков учетверяет точность формул прямоугольников и трапеций, а при использовании формулы Симпсона удвоение числа элементарных отрезков увеличивает точность в 16 раз.

6.5. Правило Рунге. Экстраполяция по Ричардсону

Отметим, что погрешность всех рассмотренных нами составных квадратурных формул удовлетворяют неравенству , где , не зависящая от h, а p – целое положительное число.

Определение. Число p называют порядком остаточного члена (погрешности) составной квадратурной формулы.

Для формулы трапеций и формулы прямоугольников p= 2. Для формулы Симпсона p = 4.