Численное интегрирование. Постановка задачи численного интегрирования, страница 4

Если выполнены условия теоремы существования и единственности и функция  непрерывна по m при , то решение задачи Коши непрерывно зависит от m.

Пример 1

При каких условиях задача Коши: ,    ,       .

является корректно поставленной?

Решение

Достаточно, чтобы функции p(x) и m(x) были непрерывны на отрезке :

,       .

Если p(x) и m(x) непрерывны на , то  тоже непрерывна. Так как m(x) непрерывна на , то существует M > 0 такое, что

   для    .

Следовательно, решение задачи Коши существует, единственно и непрерывно зависит от входных данных, то есть задача Коши является корректно поставленной.

Численные методы применимы к корректно поставленным задачам. В некоторых случаях условий корректности недостаточно. Необходимо, чтобы задача Коши была устойчива, то есть малые изменения в задании исходных данных приводили к достаточно малым измерениям искомого решения.

Пример 2

Задача Коши: ,    ,    ,     является корректно поставленной и устойчивой.

Пример 3

Задача Коши: ,    ,    ,     является корректно поставленной и неустойчивой.

Таким образом, корректно поставленная задача Коши может быть устойчивой, а может быть и неустойчивой. Устойчивость задачи Коши определяется знаком производной . Если , то задача Коши является устойчивой.

Отметим, что численные методы применимы как к устойчивым, так и к неустойчивым задачам Коши.

7.3. Метод сеток

Метод сеток – это метод, предназначенный для приближенного решения корректных дифференциальных задач. В методе сеток по исходной корректной дифференциальной задаче Ly = f строится некоторая разностная задача , а затем ищется точное решение разностной задачи. Как правило, разностная задача – это система линейных уравнений. При выполнении некоторых условий точное решение разностной задачи  является приближённым решением дифференциальной задачи.

Как строится разностная задача? Прежде всего, область определения решения дифференциальной задачи мы заменяем конечным множеством точек, другими словами вводим сетку. Для задачи Коши на отрезке  вводим сетку:

.

Решением разностной задачи является функция  – сеточная функция, то есть функция, которая определена в узлах сетки. Для задачи Коши . Производные, входящие в дифференциальное уравнение, аппроксимируются разностными отношениями. Начальное условие дифференциальной задачи заменяется разностным начальным условием. Для задачи Коши разностное начальное условие .

Пример

Запишем разностную задачу Коши (явная схема Эйлера). Найти сеточную функцию , которая удовлетворяет разностному уравнению:

,              

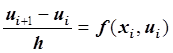и начальному условию .

Отметим, что для исходной дифференциальной задачи можно построить несколько разностных задач.

После того, как мы построили разностную задачу, ищем её точное решение. Точное решение разностной задачи при выполнении определённых условий является приближённым решением дифференциальной задачи.

Решение дифференциальной задачи – непрерывная функция, которая определена во всех точках области (в нашем случае отрезка ), а решение разностной задачи – это вектор размерности n + 1, содержащий значения сеточной функции  в узлах сетки.

7.4. Аппроксимация первой производной на равномерной сетке. Формулы численного дифференцирования

Рассмотрим несколько формул, аппроксимирующих первую производную y¢. Эти формулы можно использовать для численного дифференцирования и для построения разностных задач.

Рассмотрим равномерную сетку:

,     ,     ,     .

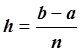Предположим, что функция  является дважды непрерывно дифференцируемой на . Тогда для первой производной справедлива формула дифференцирования вперёд:

,         .

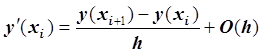Обычно под формулой численного дифференцирования понимают приближенное равенство:

.

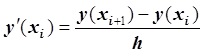Разность

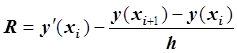
называется погрешностью аппроксимации. Если , то R = O(h), то есть , где c – константа, большая нуля, не зависящая от h. Другими словами, формула дифференцирования вперёд аппроксимирует первую производную с первым порядком по h.