Численное интегрирование. Постановка задачи численного интегрирования, страница 2

Если нам задана формула функции , то мы можем оценить погрешность, используя формулы остаточных членов. Если же формула функции  не задана, то можно использовать правило Рунге.

В вычислительной математике есть общее правило: если нам известны два приближенных значения одного и того же точного значения, то модуль разности этих двух приближенных значений, деленный на некоторую константу, является оценкой погрешности вычисления точного значения.

Правило Рунге. Разность результатов, полученных по одной и той же составной квадратурной формуле, до и после удвоения числа элементарных отрезков, можно использовать, чтобы оценить погрешность численного интегрирования.

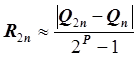, где         – значение составной квадратурной формулы для интервалов,

   – значение составной квадратурной формулы для интервала,

p        – порядок остаточного члена составной квадратурной формулы,

 – оценка погрешности численного интегрирования для  интервала; .

Для формулы прямоугольников и трапеций

.

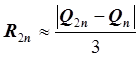Для формулы Симпсона

.

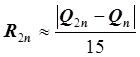Отметим, что правило Рунге используется и тогда, когда формула  задана.

Экстраполяция по Ричардсону. Пусть  и  – два приближенных значения интеграла 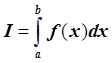 , найденных по одной и той же составной квадратурной формуле при числе отрезков n и m (m > n). Тогда более точное приближенное значение этого интеграла можно найти по формуле:

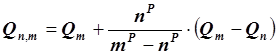, где     p – порядок остаточного члена выбранной составной квадратурной формулы;

p = 2  для формулы трапеций и формулы прямоугольников;

p = 4 для формулы Симпсона.

Если m = 2n , то  .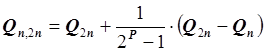

6.6. Погрешность численного интегрирования

Если задана формула , то можно использовать формулы остаточных членов (погрешности):

,

,

.

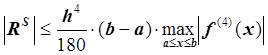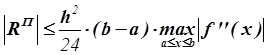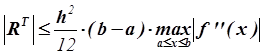Либо можно использовать правило Рунге. Считаем  и , затем находим погрешность  .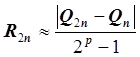

Если формула  не задана, то используем правило Рунге. Считаем , а затем  (то есть считаем, что часть  нам неизвестна).

Пример

Рассмотрим формулу трапеций при  и .

В данном случае погрешность численного интегрирования  равна модулю разности площадей двух заштрихованных треугольников, деленной на три (рис. 6.6).

Как определить число n элементарных отрезков, на которые необходимо разбить отрезок , для того, чтобы достичь точности e? Рассмотрим на примере формулы трапеций.

,                    .

,                ,        

,                 

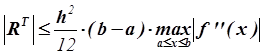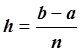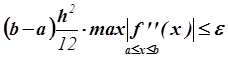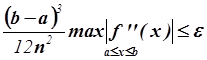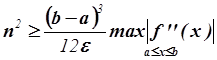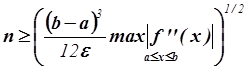
Отметим, что полученное число  является, как правило, заметно завышенным.

6.7. Численное интегрирование с неравномерным шагом

Все составные квадратурные формулы, которые мы рассматривали, записывались для случая равномерного шага. Мы также разобрали, как определить число равных отрезков n, на которые необходимо разбить отрезок , для достижения точности e.

Но на практике часто используют неравномерный шаг при численном интегрировании. Почему? Для экономии числа арифметических действий. Неравномерный шаг позволяет резко сократить объем вычислений при той же точности вычислений.

При оценке эффективности программ для численного интегрирования обычно предполагают, что большая часть стоимости счета приходится на вычисление значений подынтегральной функции . Использование неравномерного шага и позволяет резко сократить число интервалов и, следовательно, число значений функции , которые необходимо находить. Но в этом случае должна быть задана формула функции  либо алгоритм для вычисления значения  в любой точке отрезка /13/.

Рассмотрим алгоритм вычисления интеграла 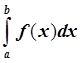  , где  может быть вычислено для любого  из отрезка [a, b] с заданной точностью.

При интегрировании с неравномерным шагом реальное число интервалов, их расположение и длины зависят от функции  и требуемой точности e.