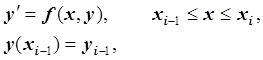
где известно точное значение ![]() . Тогда локальная погрешность
. Тогда локальная погрешность ![]() равна:
равна:
![]() , где
, где ![]() –
решение разностной задачи в отсутствие ошибок округления, а
–
решение разностной задачи в отсутствие ошибок округления, а ![]() – значение точного решения
дифференциальной задачи в точке
– значение точного решения
дифференциальной задачи в точке ![]() .
.
Глобальная погрешность – это разность между вычисленным решением разностной задачи в отсутствии ошибок округления и точным решением. То есть, решается задача Коши:
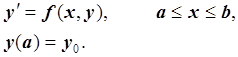
Глобальная погрешность R равна:
![]() , где
, где ![]() –
вычисленное в отсутствие ошибок округления решение разностной задачи в точке
–
вычисленное в отсутствие ошибок округления решение разностной задачи в точке ![]() ;
; ![]() –
точное решение задачи Коши в этой же точке.
–
точное решение задачи Коши в этой же точке.
Для частного случая, когда функция ![]() не
зависит от y, то есть
не
зависит от y, то есть ![]() , глобальная погрешность равна сумме
локальных погрешностей.
, глобальная погрешность равна сумме
локальных погрешностей.
В общем случае для устойчивых дифференциальных задач Коши глобальная погрешность будет меньше суммы локальных погрешностей, но для неустойчивых дифференциальных задач Коши глобальная погрешность больше суммы локальных погрешностей.
Общая погрешность – это сумма глобальной погрешности и погрешности вычислений на ЭВМ. Другими словами, общая погрешность – это разность между вычисленным и точным решениями с учетом ошибок округления на ЭВМ.
При оценке точности численного метода решения задачи Коши
важной характеристикой является порядок метода. Разностная задача имеет порядок
k по h, если для глобальной погрешности справедливо: ![]() . Для локальной погрешности в этом случае
справедливо равенство
. Для локальной погрешности в этом случае
справедливо равенство ![]() . Условия для глобальной и
локальной погрешности можно записать в эквивалентном виде:
. Условия для глобальной и
локальной погрешности можно записать в эквивалентном виде:
![]() ,
, ![]() , где c, c1
– положительные константы, не зависящие от h.
, где c, c1
– положительные константы, не зависящие от h.
Известна целая группа методов Рунге-Кутта (в последнее время в отечественной литературе начинает появляться «русский» вариант произношения фамилий авторов метода, а именно метод Рунге-Кутты), среди которых чаще всего используется метод Рунге-Кутта четвёртого порядка.
Идея метода Рунге-Кутта состоит в том, чтобы разностную задачу Коши представить в виде:
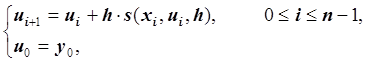
где функция s приближала бы отрезок ряда Тейлора:
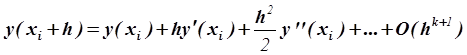
с точностью ![]() , но в то же время не содержала бы
производных функции
, но в то же время не содержала бы
производных функции ![]() . Здесь k – порядок разностной задачи.
. Здесь k – порядок разностной задачи.
Мы рассмотрим методы Рунге первого, второго и четвёртого порядков.
Метод Рунге-Кутта первого порядка (метод Эйлера)
Метод Рунге-Кутта первого порядка – это уже рассмотренная нами явная схема Эйлера (метод Эйлера):
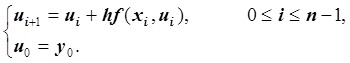
Метод Эйлера – метод первого порядка, то есть локальная
погрешность равна ![]() , глобальная погрешность равна
, глобальная погрешность равна ![]() . Метод Эйлера является одним из самых
простых методов, но в практических расчётах используется редко, так как обладает
значительной погрешностью. Разностная задача является условно устойчивой. Для
модельной дифференциальной задачи Коши:
. Метод Эйлера является одним из самых
простых методов, но в практических расчётах используется редко, так как обладает
значительной погрешностью. Разностная задача является условно устойчивой. Для
модельной дифференциальной задачи Коши:
![]()
условие устойчивости разностной
задачи ![]() .
.
Метод Эйлера легко обобщается на системы дифференциальных уравнений первого порядка.
Пример
Методом Эйлера построить алгоритм решения задачи Коши:
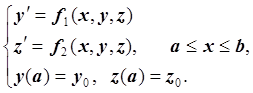
Решение
Запишем разностную задачу:
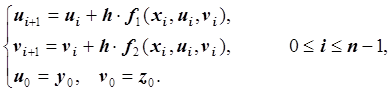
Вектора: ![]() и
и ![]() являются приближёнными решениями задачи
Коши.
являются приближёнными решениями задачи
Коши.
Метод Рунге-Кутта второго порядка
Формулы метода Рунге-Кутта второго порядка (метода Эйлера-Коши, модифицированного метода Эйлера) записывается следующим образом:
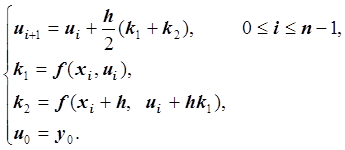
Порядок метода – второй, то есть локальная погрешность
равна: ![]() , глобальная погрешность
, глобальная погрешность ![]() . Разностная задача является условно
устойчивой. Для модельной дифференциальной задачи Коши:
. Разностная задача является условно
устойчивой. Для модельной дифференциальной задачи Коши:
![]() ;
;
условие устойчивости разностной
задачи ![]() .
.
Метод Рунге-Кутта четвёртого порядка
Чаще всего на практике используется метод Рунге-Кутта четвёртого порядка.
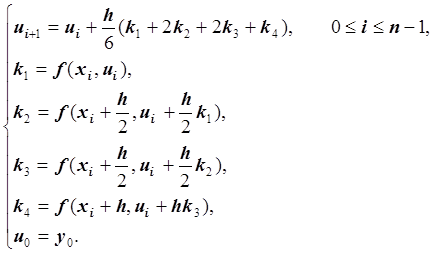
Порядок метода – четвёртый. Локальная погрешность равна: ![]() , глобальная погрешность
, глобальная погрешность ![]() . Разностная задача является условно
устойчивой. Для модельной дифференциальной задачи Коши:
. Разностная задача является условно
устойчивой. Для модельной дифференциальной задачи Коши:
![]()
условие устойчивости разностной
задачи ![]() .
.
Метод Рунге-Кутта четвёртого порядка легко распространяется на системы дифференциальных уравнений первого порядка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.