Отметим важное свойство методов Рунге-Кутта. Эти методы являются самостартующими. Самостартующий метод – это численный метод, в котором для начала вычислений не требуется дополнительных расчётов.
Для оценки погрешности методов Рунге-Кутта используют
двойной пересчёт на ЭВМ. Сначала находится приближённое решение ![]() на отрезке
на отрезке ![]() с шагом
h, а затем расчёт проводится на
этом же отрезке в два этапа с шагом h/2,
и получается приближенное решение
с шагом
h, а затем расчёт проводится на
этом же отрезке в два этапа с шагом h/2,
и получается приближенное решение ![]() . Величина
. Величина
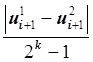 , где k – это порядок разностной задачи, является оценкой
погрешности.
, где k – это порядок разностной задачи, является оценкой
погрешности.
При реальных вычислениях используется, как правило, переменный шаг, что позволяет добиться требуемой точности с минимальным количеством узлов сетки. Двойной пересчёт на ЭВМ используется в этом случае как для контроля за погрешностью, так и для определения величины шага.
Метод Милна – это один из методов прогноза и коррекции
(предиктор-корректор, счёт-пересчёт). Приближённое решение ![]() находится в два этапа. На первом шаге находится
находится в два этапа. На первом шаге находится
![]() (прогноз), которое можно рассматривать как
достаточно грубое приближение, а на втором шаге
(прогноз), которое можно рассматривать как
достаточно грубое приближение, а на втором шаге ![]() (прогноз)
уточняется и находится
(прогноз)
уточняется и находится ![]() (коррекция). Обозначим
(коррекция). Обозначим ![]() (прогноз) и
(прогноз) и ![]() (коррекция).
(коррекция).
Запишем формулы двух этапов метода Милна:
этап прогноза
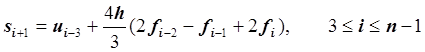 , где для компактности записи
использовано следующее обозначение
, где для компактности записи
использовано следующее обозначение ![]() .
.
этап коррекции
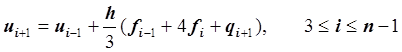
где ![]() .
.
Порядок метода Милна – четвёртый.
Метод Милна не является самостартующим , для начала
вычислений необходим начальный отрезок ![]() .
Значение
.
Значение ![]() известно из начального условия, а величины
известно из начального условия, а величины
![]() находятся каким-либо самостартующим
методом, имеющим тот же порядок, что метод Милна. Как правило, эти значения
находят методом Рунге-Кутта четвёртого порядка.
находятся каким-либо самостартующим
методом, имеющим тот же порядок, что метод Милна. Как правило, эти значения
находят методом Рунге-Кутта четвёртого порядка.
Мы уже говорили о том, что если мы имеем два приближения к
одному значению, то модуль разности этих приближений, делённый на некоторую
константу, является оценкой погрешности приближения. Это правило
распространяется и на метод Милна. Погрешность метода Милна ![]() оценивается по формуле:
оценивается по формуле:
 , где
, где ![]() (коррекция),
а
(коррекция),
а ![]() (прогноз).
(прогноз).
Задача 1
Функция
![]() задана таблично:
задана таблично:
|
x |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
|
y |
0 |
0.04 |
0.16 |
0.36 |
0.64 |
1.00 |
Вычислить значения первой производной функцииy в точках 0., 0.6, 1.0 с первым и со вторым порядком точности по h.
Решение
Для вычисления приближенных значений первой производной с первым порядком по h воспользуемся формулами численного дифференцирования, а именно, формулой дифференцирования вперёд и формулой дифференцирования назад:
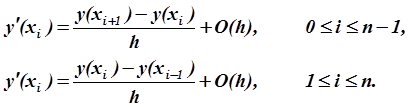
Получаем:
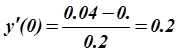 ,
,
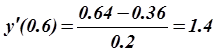 ,
,
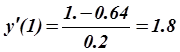 .
.
Отметим, что для вычисления ![]() с
первым порядком по h мы
воспользовались формулой дифференцирования вперёд, но можно было
воспользоваться формулой дифференцирования назад.
с
первым порядком по h мы
воспользовались формулой дифференцирования вперёд, но можно было
воспользоваться формулой дифференцирования назад.
Для вычисления ![]() во внутренней точке x = 0.6 со вторым порядком по h используется центральная разность:
во внутренней точке x = 0.6 со вторым порядком по h используется центральная разность:
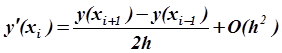 , а
для вычисления
, а
для вычисления ![]() на концах отрезка со вторым
порядкм по h применяются формулы:
на концах отрезка со вторым
порядкм по h применяются формулы:
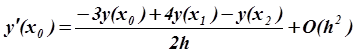 ,
,
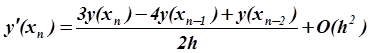 .
.
Получаем:
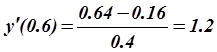 ,
, 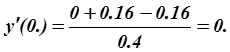 ,
,
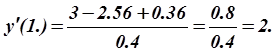
Задача 2
Методом Эйлера с шагом h = 0.1 построить алгоритм для решения задачи Коши:
![]()
Решение
Запишем разностную задачу Коши:

Шаг h = 0.1;
значения ![]() ; число
; число 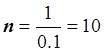 .
.
Вектор ![]() является
приближённым решением задачи Коши.
является
приближённым решением задачи Коши.
Задача 3
Методом Рунге-Кутта второго порядка с шагом h = 0.1 построить алгоритм для решения задачи Коши:
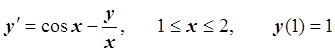
Решение
Запишем разностную задачу Коши:
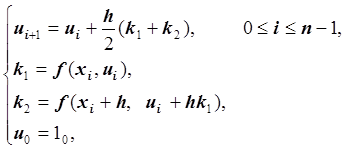
где 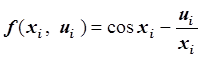 , шаг
h = 0.1,
, шаг
h = 0.1, ![]() ,
,
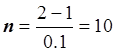 .
.
Вектор ![]() является
приближённым решением задачи Коши.
является
приближённым решением задачи Коши.
Задача 4
Методом Рунге-Кутта четвёртого порядка с шагом h = 0.1 построить алгоритм для решения задачи Коши:
![]()
Решение
Запишем разностную задачу Коши:
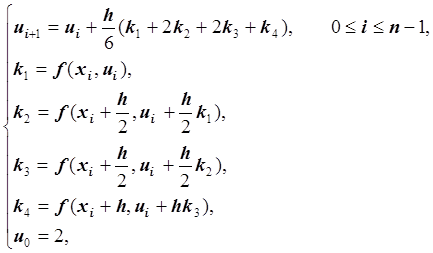
где ![]() ;
шаг h = 0.1;
;
шаг h = 0.1; ![]() ;
; 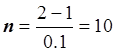 .
.
Вектор ![]() является
приближённым решением задачи Коши.
является
приближённым решением задачи Коши.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.