Численное интегрирование. Постановка задачи численного интегрирования, страница 3

В этом случае сначала вычисляется приближённое значение  на отрезке ,  . Затем отрезок делится пополам, и вычисляется  на этом же отрезке, но в два этапа. Оценивается погрешность по правилу Рунге. Если погрешность удовлетворяет неравенству: 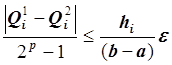  ,   то переходим к следующему отрезку, в противном случае снова делим отрезок пополам и т.д.

6.8. Примеры решение задач

Задача 1

Значение интеграла на отрезке [0, 1], вычисленное по формуле Симпсона с шагом , оказалось равным 10.4, а с шагом  –  равным 10.5. Используя экстраполяцию по Ричардсону, уточнить результат. Оценить погрешность по правилу Рунге.

Решение

Экстраполяция по Ричардсону

 ,,  .

.

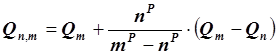Отметим, что формула записана в обозначениях  n, m, а задача сформулирована в обозначениях , нужно перейти  к :

,           ,            ,            ;

,         ,                 ,        ,        ;

,            .

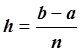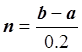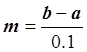Для формулы трапеций и формулы прямоугольников p = 2, для формулы Симпсона p = 4.

.

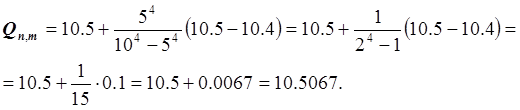
Оценим погрешность по правилу Рунге      .

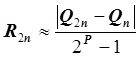,     где     ,       ;           .

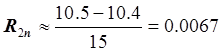Ответ: ,         .

Задача 2

Что больше: значение составной квадратурной формулы трапеций или значение интеграла?

Решение

.

Задача составлена таким образом, что для формулы трапеции и прямоугольников  не меняет знак на , а для формулы Симпсона  не меняет знак на :

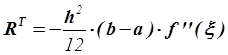, так как ,   , следовательно,  знак   определяется знаком  на .

Если  на  для всех , то .

Если  на  для всех , то .

,  ,  ,

  на  , следовательно,  .

,                        .

Если  ,    ,               то        .

Ответ:  Значение интеграла меньше, чем значение составной квадратурной формулы трапеций   .

Задача 3

Определить число равных отрезков n, на которые необходимо разбить отрезок  для вычисления интеграла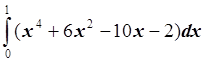 по формуле  трапеций с тремя верными десятичными знаками.

Решение

Трём верным десятичным знакам соответствует абсолютная погрешность e = 0.0005, двум верным десятичным знакам – e = 0.005, четырём – e = 0.00005.

,     ,      ,

.

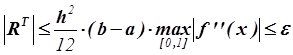, следовательно, .

,                     .

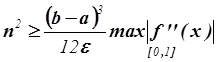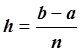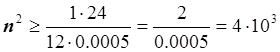,           ,             n = 67.

Ответ. n = 67.

Задача 4

Используя формулу Симпсона, построить алгоритм для вычисления интеграла 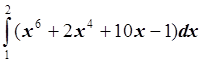    с двумя верными десятичными знаками.

Решение

Прежде всего, отметим, что двум верным десятичным знакам соответствует абсолютная погрешность.

Необходимо найти число равных отрезков n, на которые нужно разбить  для вычисления интеграла с точностью e по формуле Симпсона:

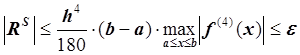, следовательно,

;

,      ,     ,

,     ;

;

;

,            ,           .

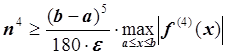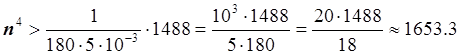Для формулы Симпсона n должен быть четным:  n = 2m.

Построим алгоритм. Число отрезков равно:   ,      .

Найдём приближенное значение:

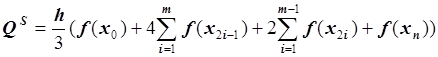, где

,               .

Сетка  ,     ,   ,     ,    .

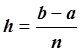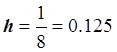7. Численные методы решения задачи Коши для обыкновенного дифференциального уравнения первого порядка

Рассмотрим обыкновенное дифференциальное уравнение первого порядка . Это дифференциальное уравнение имеет бесконечное множество решений, но для него можно поставить задачу Коши, которая при определённых условиях имеет единственное решение.

7.1. Постановка задачи Коши

Найти дифференцируемую на отрезке  функцию , удовлетворяющую дифференциальному уравнению:

,        

и начальному условию , где  – непрерывная заданная функция.

Предполагается, что функция  определена для всех  при x из отрезка.

Рекомендуемая литература: /4, 9-10, 12, 13/.

7.2. Корректность задачи Коши и устойчивость

Сформулируем условия, при которых задача Коши имеет единственное решение.

Теорема (существования и единственности)

Если функция непрерывна в прямоугольнике  и удовлетворяет в области D условию , где M – константа большая нуля, то задача Коши имеет единственное решение. Это решение непрерывно зависит от начального условия .