Численное интегрирование. Постановка задачи численного интегрирования, страница 5

Используя формулу дифференцирования вперёд, запишем разностную задачу (разностную схему) для дифференциальной задачи Коши:

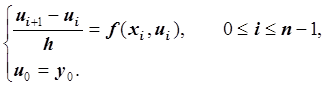
Эта разностная задача называется явной схемой Эйлера.

Аналогично дифференцированию вперёд для дважды непрерывно дифференцируемой на  функции y справедлива формула дифференцирования назад:

,           .

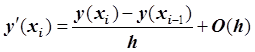Получаем приближённое равенство:

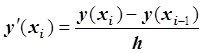, которое является формулой численного дифференцирования. Для  погрешность аппроксимации R = O(h), то есть , где c – константа, большая нуля, не зависящая от h. Другими словами, формула дифференцирования назад аппроксимирует первую производную с первым порядком по h.

Используя формулу дифференцирования назад, запишем разностную задачу (разностную схему) для дифференциальной задачи Коши:

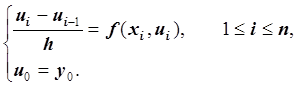
Эта разностная задача называется явной схемой Эйлера.

Термин «явная» и «неявная» схемы связаны с тем, что явная схема, например явная схема Эйлера, даёт возможность найти  по явной формуле:

, где  – известная величина. В случае неявной схемы получается уравнение, в котором неизвестное  входит и в левую, и в правую часть:

.

Явные схемы удобны тем, что по ним легко находятся неизвестные значения .

Формулу дифференцирования вперёд называют ещё правой разностью, формулу дифференцирования назад – левой разностью. А для  справедлива формула численного дифференцирования, называемая центральной разностью:

,    .

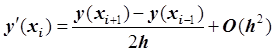Центральная разность аппроксимирует первую производную со вторым порядком по h.

Запишем формулы, аппроксимирующие первую производную со вторым порядком по h на концах отрезка (в точках  и ):

,

.

7.5. Устойчивость разностных задач

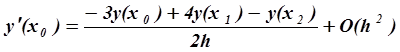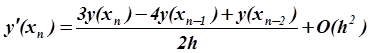Одной из важных характеристик разностной задачи является устойчивость или неустойчивость разностной задачи. Устойчивость разностной задачи – это внутреннее свойство разностной задачи, никак не связанное с исходной дифференциальной задачей. Для устойчивой дифференциальной задачи мы можем построить как устойчивую разностную задачу, так и неустойчивую.

Как понимается устойчивость разностной задачи? Малые возмущения во входных данных устойчивой разностной задачи приводят к малым возмущениям в её решении. Для разностной задачи Коши входными данными являются начальное условие  и правая часть .

Разностные задачи бывают: безусловно устойчивыми, условно устойчивыми и неустойчивыми. Разностная задачи называется условно устойчивой, если она устойчива лишь при выполнении некоторого условия на величину шага h. Если разностная задача устойчива при любых h, то её называют безусловно (абсолютно) устойчивой.

Практическое правило. Явные разностные задачи (схемы), как правило, условно устойчивы, а неявные разностные задачи, как правило, безусловно устойчивы.

Для численного решения задачи Коши мы будем рассматривать только явные разностные схемы, и все они будут условно устойчивыми. При нарушении условия устойчивости разностной задачи, то есть при неверном выборе h, вычисленное решение может существенно отличаться от точного. В некоторых случаях при вычислениях на ЭВМ может возникнуть «машинное переполнение», то есть выход за границы действительных чисел, с которыми оперирует ЭВМ.

Устойчивость разностных задач Коши рассматривается, как правило, для модельной дифференциальной задачи Коши:

,                   ,

, где m – константа, m > 0. Для этой модельной задачи удаётся записать условия устойчивости для различных разностных задач.

7.6. Погрешности численных методов

При рассмотрении численных методов решения задачи Коши выделяют следующие погрешности

1)  локальную (ошибку);

2)  глобальную (ошибку);

3)  вычислений на ЭВМ;

4)  общую.

Локальная погрешность – это погрешность, допущенная на данном шаге , при условии, что предыдущие значения вычислены точно и отсутствуют ошибки округления. Другими словами, решается задача Коши: