
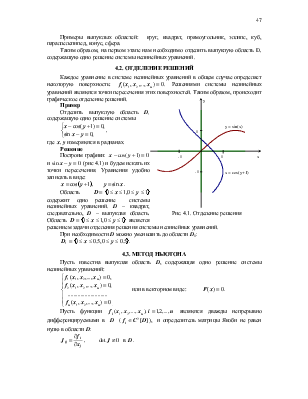




















Пусть задана система нелинейных уравнений:
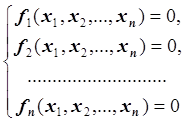 или
в векторном виде: F(x) = 0.
или
в векторном виде: F(x) = 0.
Требуется найти приближенное значение решения системы нелинейных уравнений такое, что
![]() , где
, где ![]() –
приближенное решение; c – точное
решение.
–
приближенное решение; c – точное
решение.
Рекомендуемая литература: /2-4, 5, 6/.
Задача может ставиться по-разному: найти все решения, найти хотя бы одно решение. Отметим, что решение системы нелинейных уравнений является существенно более сложной задачей, чем решение системы линейных уравнений. Для системы нелинейных уравнений возможны четыре случая:
1) система нелинейных уравнений имеет единственное решение;
2) система нелинейных уравнений не имеет решения;
3) система нелинейных уравнений имеет бесконечное множество решений;
4) система нелинейных уравнений имеет несколько решений.
Вопрос о существовании и количестве решений системы нелинейных уравнений в общем случае является сложным. Приведём пример из /3/.
Пример
Рассмотрим систему нелинейных уравнений:
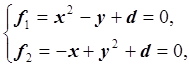
где d – вещественный параметр, -1 £ d £ 1. Если изменять d в указанном интервале, то имеют место следующие случаи:
1) d = -1 – четыре решения;
2) d = 0 – два решения;
3) d = 0.25 – решение единственно;
4) d = 1 – решений нет.
Как и при решении одного нелинейного уравнения задача разбивается на две подзадачи:
1) отделение решения, то есть
нахождение некоторых областей Di, каждая из которых
содержит одно и только одно решение системы нелинейных уравнений, ![]() , где m
– число решений системы нелинейных уравнений;
, где m
– число решений системы нелинейных уравнений;
2) в известной области D, содержащей одно решение системы нелинейных уравнений, ищется приближенное решение с заданной точностью e. Этот этап называется уточнением решения.
Отметим, что мы будем рассматривать два итерационных метода – метод итераций и метод Ньютона. Оба эти метода можно использовать тогда, когда известна выпуклая область D, содержащая одно решение системы нелинейных уравнений.
Определение. Область называется выпуклой, если отрезок прямой, соединяющий две любые точки области, полностью принадлежит области.
Примеры выпуклых областей: круг, квадрат, прямоугольник, эллипс, куб, параллелепипед, конус, сфера.
Таким образом, на первом этапе нам необходимо отделить выпуклую область D, содержащую одно решение системы нелинейных уравнений.
 Каждое уравнение в системе нелинейных уравнений в общем случае
определяет некоторую поверхность:
Каждое уравнение в системе нелинейных уравнений в общем случае
определяет некоторую поверхность: ![]() . Решениями системы
нелинейных уравнений являются точки пересечения этих поверхностей. Таким
образом, происходит графическое отделение решений.
. Решениями системы
нелинейных уравнений являются точки пересечения этих поверхностей. Таким
образом, происходит графическое отделение решений.
Пример
Отделить выпуклую область D, содержащую одно решение системы
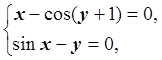 ,
,
где х, y измеряются в радианах.
Решение
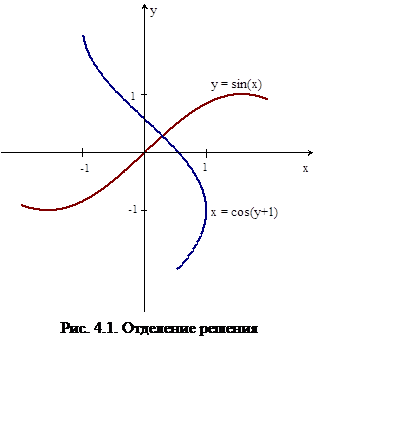
Построим графики:
![]() и
и ![]() (рис
4.1) и будем искать их точки пересечения. Уравнения удобно записать в виде:
(рис
4.1) и будем искать их точки пересечения. Уравнения удобно записать в виде:
![]() ,
, ![]() .
.
Область ![]() содержит одно решение
системы нелинейных уравнений. D –
квадрат, следовательно, D –
выпуклая область. Область
содержит одно решение
системы нелинейных уравнений. D –
квадрат, следовательно, D –
выпуклая область. Область ![]() является решением
задачи отделения решения системы нелинейных уравнений.
является решением
задачи отделения решения системы нелинейных уравнений.
При необходимости D можно уменьшить до области D1:
![]() .
.
Пусть известна выпуклая область D, содержащая одно решение системы нелинейных уравнений:
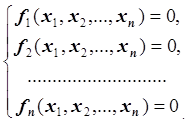 или
в векторном виде:
или
в векторном виде: ![]() .
.
Пусть функции ![]() являются дважды
непрерывно дифференцируемыми в D (
являются дважды
непрерывно дифференцируемыми в D (![]() ), и определитель матрицы Якоби
не равен нулю в области D:
), и определитель матрицы Якоби
не равен нулю в области D:
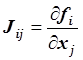 ,
, ![]() в D.
в D.
Тогда можно построить
последовательность ![]() , каждый элемент которой является
вектором размерности n:
, каждый элемент которой является
вектором размерности n: ![]() , и которая определяется по формуле:
, и которая определяется по формуле:
![]() , где
, где ![]() .
.
Неудобство этой формулы заключается в необходимости
вычисления обратной матрицы. Из теории систем линейных уравнений мы помним,
что, с точки зрения вычислительной математики, решение систем линейных
уравнений проще и устойчивее, чем обращение матрицы. Так как ![]() , то умножим обе части на
, то умножим обе части на ![]() и получим:
и получим:
![]() или
или ![]() .
.
То есть мы получили систему
линейных уравнений: ![]() , где
, где ![]() ,
, ![]() ,
, ![]() . Здесь
. Здесь ![]() –
неизвестный вектор,
–
неизвестный вектор, ![]() – известный вектор.
– известный вектор.
Условие сходимости метода Ньютона сформулируем нестрого.
Если вектор начального приближения ![]() выбран достаточно близко к точному
решению, то последовательность
выбран достаточно близко к точному
решению, то последовательность ![]() , построенная методом Ньютона,
сходится к точному решению системы нелинейных уравнений.
, построенная методом Ньютона,
сходится к точному решению системы нелинейных уравнений.
Условие остановки итерационного процесса:
![]() .
.
Из этого условия вытекает, что ![]() , где с – точное решение системы нелинейных уравнений; p –
положительная константа, не зависящая от e.
, где с – точное решение системы нелинейных уравнений; p –
положительная константа, не зависящая от e.
Пример
Построить
алгоритм решения системы нелинейных уравнений методом Ньютона с точностью
![]() :
:
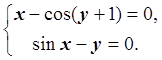
Решение
1. В примере (разд. 4.2) мы отделили выпуклую область: ![]() , содержащую одно решение системы
нелинейных уравнений. В нашем случае:
, содержащую одно решение системы
нелинейных уравнений. В нашем случае:
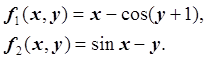
Функции ![]() дважды непрерывно
дифференцируемы в области D.
Построим матрицу Якоби:
дважды непрерывно
дифференцируемы в области D.
Построим матрицу Якоби:
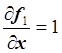 ,
, 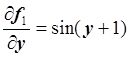 ,
,
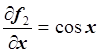 ,
, 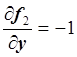 ,
, 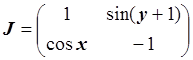 .
.
Найдём определитель матрицы Якоби (якобиан) и докажем, что он не равен нулю в области D:
![]() .
.
Докажем, что выражение ![]() не
принимает значение -1 в области D:
не
принимает значение -1 в области D:
при ![]() ,
, ![]() , при
, при ![]() ,
, ![]() , следовательно,
, следовательно, ![]() ,
, ![]() .
.
2. При выполнении этих условий можно применять метод Ньютона:
![]() .
.
Запишем формулу метода Ньютона в развёрнутом виде:
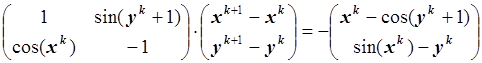 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.