Итерационные методы решения систем нелинейных уравнений, страница 8

Решение

Сначала нужно построить  в виде: 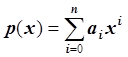  . Так как размерность таблицы равна 3,       то             .

Запишем систему линейных уравнений для нахождения  неизвестных :

                  

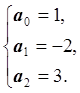
Запишем интерполяционный полином: .

Проверим результат:           ,          ,        .

Теперь нужно  представить в виде суммы полиномов Чебышева:

.

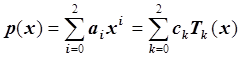Известно, что   ,          .       найдем по рекуррентной формуле:

;

Выражаем      через полиномы Чебышева:

,           ,              .

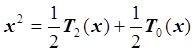Запишем  в общем виде:

.

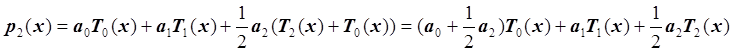Для нашего случая: .

Число M можно найти двумя способами. В общем случае:

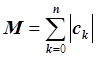 или .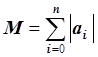

В нашем случае:

Ответ: ,    M = 6.

4. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ......................................................................... 46

4.1. Постановка задачи.................................................................................................................................................................................................... 46

4.2. Отделение решений................................................................................................................................................................................................... 47

4.3. Метод Ньютона......................................................................................................................................................................................................... 47

4.4. Метод итераций......................................................................................................................................................................................................... 49

4.5. Примеры решения задач.......................................................................................................................................................................................... 53

5. Интерполяция полиномами........................................................................................................................................................................ 56

5.1. Интерполяционная таблица................................................................................................................................................................................... 56

5.2. Постановка задачи интерполяции........................................................................................................................................................................ 57

5.3. Существование и единственность  интерполяционного полинома............................................................................................................ 57

5.4. Оценка погрешности интерполяции полиномами............................................................................................................................................ 58

5.5. Интерполяционный полином Лагранжа............................................................................................................................................................. 58

5.6. Сходимость интерполяционных полиномов..................................................................................................................................................... 59

5.7. Выбор узлов интерполяции.................................................................................................................................................................................... 60

5.8. Примеры решения задач.......................................................................................................................................................................................... 62