Итерационные методы решения систем нелинейных уравнений, страница 6

Пример 2 (Бернштейн, 1912 г.)

Последовательность интерполяционных 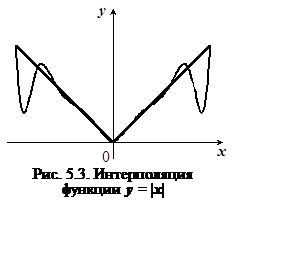полиномов , построенных на равномерных сетках ,  для непрерывной функции , не стремится с возрастанием n к функции  ни в одной точке отрезка , отличной от  -1, 0,1 (рис. 5.3).

Эти два примера иллюстрируют недостаток интерполяции полиномами:  с увеличением степени интерполяционного полинома возможны существенные отклонения интерполяционного полинома от функции на концах интервала. Увеличение степени полинома накладывает все более жесткие ограничения на  .

Теорема Фабера

Для любой интерполяционной таблицы размерности  найдутся непрерывная функция  и точка , такие, что  не сходится к функции  в точке  при .

5.7. Выбор узлов интерполяции

Мы уже говорили, что сетки могут быть равномерными и неравномерными. Возникает естественный вопрос: существует ли оптимальное распределение узлов на отрезке  при интерполяции полиномами? То есть существует ли распределение узлов, при котором погрешность интерполяции полиномами минимальна при фиксированном n?

Отметим, что во многих задачах вычислительной математики введение неравномерной сетки позволяет уменьшить погрешность или сделать ее минимальной. Таким образом в вычислительной математике существует общий прием – введение неравномерной сетки.

Рассмотрим применение этого приема при интерполяции полиномами. Рассмотрим оценку погрешности:

.

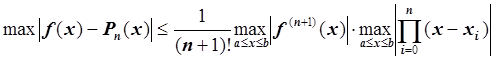Первые два сомножителя не зависят от  .

От  зависит третий сомножитель 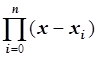, полином степени . То есть нужно решить задачу:

.

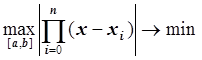Если в качестве  рассмотреть отрезок , то мы получим задачу, которая решается с помощью полиномов Чебышева. Оптимальным распределением узлов интерполяции на отрезке [-1, 1] являются нули полинома Чебышева .

Полиномы Чебышева определяются следующим образом:

,      .

Запишем полиномы Чебышева степени 0 и степени 1:    ,         . Полиномы более высокой степени вычисляются по рекуррентной формуле:

.

Найдем нули полинома Чебышева степени n:.

,               ,       

,            .

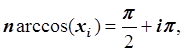
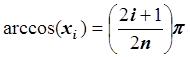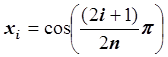Запишем формулу для нулей полинома Чебышева степени n таким образом, чтобы  вычислялись в порядке возрастания:

,             .

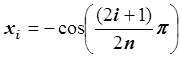Точки  являются оптимальными узлами сетки размерности  n при интерполяции полиномами на отрезке [-1, 1]. Из формулы для нулей полинома Чебышева вытекает, что  для любого i, то есть   на отрезке [-1, 1] имеет n вещественных корней.

Если интерполирование производится на отрезке [a, b], то линейной заменой переменных

 

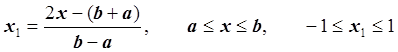
переводим отрезок [a, b] в отрезок [-1, 1].

Отметим  два свойства полиномов Чебышева:

1) старший коэффициент  равен;

2)  – это ортогональные полиномы на отрезке [-1, 1] с весом 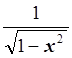, т.е.

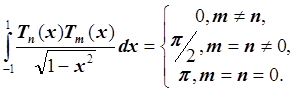
Теорема Чебышева

Из всех полиномов  n-й степени со старшим коэффициентом, равным единице, для полинома 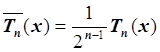    выполнено неравенство:

,

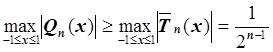то есть полиномы   – это полиномы, наименее уклоняющиеся от нуля в равномерной норме на отрезке [-1, 1].

Сформируем два важных утверждения, связанных с оптимальным выбором узлов интерполяции. Первое утверждение – это оценка погрешности для оптимального распределения узлов. Второе утверждение – это теорема о сходимости интерполяционных полиномов при оптимальном распределении узлов.

Теорема (оценка погрешности)

Если в качестве узлов интерполяции на отрезке [-1, 1] выбраны нули полинома Чебышева  степени n + 1, то для интерполяционного полинома , построенного по соответствующей интерполяционной таблице, справедлива оценка погрешности:

.

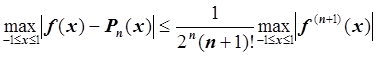Если же интерполяция проводится на отрезке [a, b] и в качестве узлов интерполяции выбраны точки, соответствующие нулям полинома Чебышева на отрезке [-1, 1], то справедлива оценка:

.

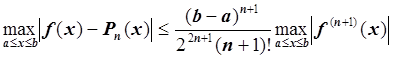Теорема  (о сходимости)