Заметим, что это гарантирует сходимость метода итераций,
но сходимость будет медленной. Метод итераций быстро сходится, если ![]() .
.
Для улучшения сходимости можно еще уменьшить D или выбрать ![]() и
и
![]() другим способом.
другим способом.
2. Выбираем точку начального приближения из D: ![]() .
.
Так как ![]() , то последовательность
, то последовательность ![]() сходится к точному решению.
сходится к точному решению.
3. Строим итерационный процесс:
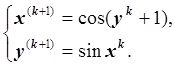
4. Условие остановки итерационного процесса: 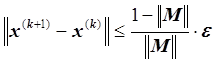 .
.
Вектор ![]() , удовлетворяющий этому
условию, является приближенным решением, полученным методом итераций, с
точностью e.
, удовлетворяющий этому
условию, является приближенным решением, полученным методом итераций, с
точностью e.
Недостатки метода итераций
1. Нет общего приема для перехода от системы F(x) = 0 к системе x = F(x).
2. Метод медленно сходится для M таких, что ![]() .
.
Устойчивость метода итерации. Если ![]() , то метод итераций является устойчивым
относительно вычислительной погрешности.
, то метод итераций является устойчивым
относительно вычислительной погрешности.
Пример 2
Известно, что решение системы нелинейных уравнений:
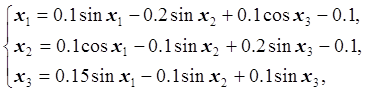 (где
(где ![]() измеряются
в радианах)
измеряются
в радианах)
принадлежит области ![]() . Построить и обосновать алгоритм решения системы нелинейных уравнений методом итераций с
точностью e.
. Построить и обосновать алгоритм решения системы нелинейных уравнений методом итераций с
точностью e.
Решение
Область D – куб, следовательно, D – выпуклая область, содержащая одно решение системы нелинейных уравнений. Система уже приведена к виду, удобному для итераций:
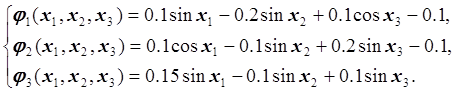
Функции ![]() являются непрерывно
дифференцируемыми в области D. Найдем
элементы матрицы М и вычислим
являются непрерывно
дифференцируемыми в области D. Найдем
элементы матрицы М и вычислим ![]() :
:
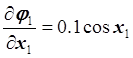 ,
, 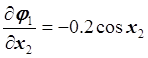 ,
, 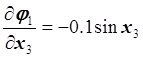 ,
,
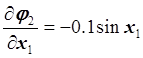 ,
, 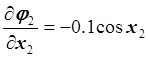 ,
, 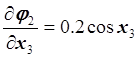 ,
,
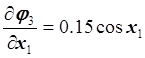 ,
, 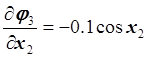 ,
, 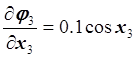 ;
;
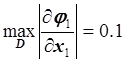 ,
, 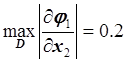 ,
, 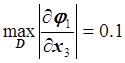 ,
,
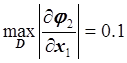 ,
, 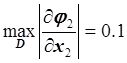 ,
, 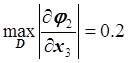 ,
,
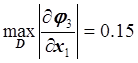 ,
, 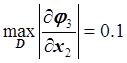 ,
, 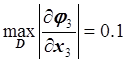 ;
;
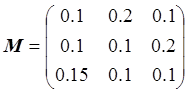 ,
, ![]() .
.
![]() , следовательно, метод итераций
сходится для любого начального приближения
, следовательно, метод итераций
сходится для любого начального приближения ![]() .
.
2. Начальное приближение: ![]() .
.
3. Формулы метода:
![]() ,
,
![]() ,
,
![]() .
.
Так как ![]() , то последовательность
, то последовательность ![]() , где
, где ![]() ,
сходится к точному решению системы нелинейных уравнений.
,
сходится к точному решению системы нелинейных уравнений.
4. Условие остановки итерационного процесса:
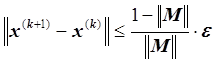 ,
, ![]() .
.
Вектор ![]() , удовлетворяющий
условию остановки итерационного процесса, считается приближенным
решением системы нелинейных уравнений, полученным методом итераций с точностью
e.
, удовлетворяющий
условию остановки итерационного процесса, считается приближенным
решением системы нелинейных уравнений, полученным методом итераций с точностью
e.
Задача 1
Построить и обосновать алгоритм решения системы нелинейных уравнений методом Ньютона с точностью e.
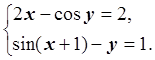
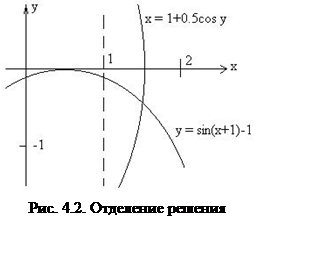 Решение
Решение
Графическое отделение решения
Запишем в удобном виде: ![]() ,
, ![]() , построим графики (рис. 4.2) и найдем
точки пересечения.
, построим графики (рис. 4.2) и найдем
точки пересечения.
Область, содержащая одно решение: D = { 1 £ x £ 1.6; – 1 £ y £ 0 }. D – прямоугольник, следовательно, выпуклая область.
Алгоритм метода Ньютона
Выпуклая область D содержит одно решение системы:
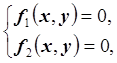
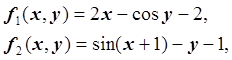
1. Функции f1, f2 являются дважды непрерывно дифференцируемыми в области D. Запишем матрицу Якоби:
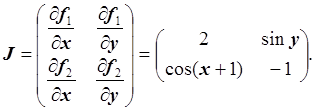
Вычислим определитель матрицы Якоби: ![]() .
.
Якобиан не равен нулю, так как sin y cos (x + 1) ¹ – 2 для всех x, y из области D:
sin y | £ 1, | cos (x + 1) | £ 1.
Для уточнения решения в области D можно использовать метод Ньютона.
2. Формула метода:
![]() ,
, ![]() ;
;
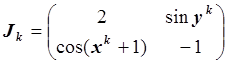 ,
, 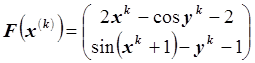 .
.
Получили систему линейных уравнений с невырожденной матрицей. Для каждого k необходимо решать систему линейных уравнений. Для этого используется метод Гаусса с частичным выбором ведущего элемента.
3. Точка начального приближения: x(0) = (1, 0).
4. Условие остановки итерационного процесса: ![]() .
.
Вектор ![]() , для которого выполняется условие
остановки итерационного процесса, является приближенным решением,
полученным методом Ньютона.
, для которого выполняется условие
остановки итерационного процесса, является приближенным решением,
полученным методом Ньютона.
Задача 2
Построить и обосновать алгоритм решения системы нелинейных уравнений методом итераций с точностью e:
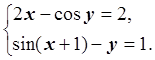
Решение
В задаче 1 мы уже отделили выпуклую область: D = { 1 £ x £ 1.6; – 1 £ y £ 0 }, содержащую одно решение системы.
1. По системе ![]() построим эквивалентную
систему
построим эквивалентную
систему ![]() :
:
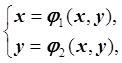
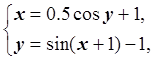
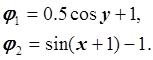
Функции ![]() являются непрерывно
дифференцируемыми в области D.
являются непрерывно
дифференцируемыми в области D.
Построим матрицу М:
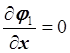 ,
, 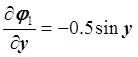 ,
, 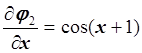 ,
, 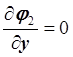 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.