Итерационные методы решения систем нелинейных уравнений, страница 5

5.2. Постановка задачи интерполяции

Пусть на отрезке [a, b] задана сетка  , в узлах которой заданы значения: ,   (где  – некоторая функция). Требуется построить функцию  такую, что

1) ,               ;

2)  достаточно близка к  на отрезке [a, b].

Отметим, что в литературе известны другие, близкие к этой, постановки задачи. Во многих постановках задачи сразу требуется, чтобы  была непрерывной функцией, часто опускается второе условие.

Задача интерполяции имеет множество решений, если нет определённых ограничений для функции , в противном случае можно получить задачу, имеющую единственное решение. При интерполяции возникает два основных вопроса:

1) Как построить?

2) Как оценить погрешность: ?

Рассмотрим частный случай, когда  – полином степени n, то есть

.

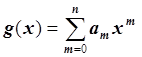Интерполяция полиномами достаточно естественна и опирается на аппроксимационную теорему Вейерштрасса (1885 г).

Теорема

Если непрерывная функция на конечном замкнутом интервале , то  для любого  существует полином  степени  такой, что

.

Но отметим очень важный факт: в теореме говорится о некотором полиноме степени n, а не об интерполяционном полиноме.

5.3. Существование и единственность интерполяционного полинома

Рассмотрим вопрос о существовании и единственности интерполяционного полинома.

Теорема (существования и единственности)

Пусть на отрезке [a, b] задана сетка , в узлах которой заданы значения ,  ,  при . Тогда существует единственный полином  степени n такой, что

.

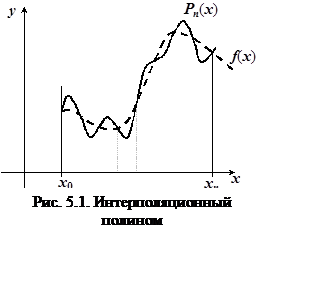Таким образом, по любой интерполяционной таблице, у которой все  различны между собой, всегда можно построить единственный интерполяционный полином, степень которого на единицу меньше, чем размерность интерполяционной таблицы (рис. 5.1).

5.4. Оценка погрешности интерполяции полиномами

Теперь обсудим погрешность интерполяционного полинома.

Теорема (оценка погрешности)

Пусть  n + 1 раз непрерывно дифференцируема на отрезке [a, b],  – интерполяционный полином на интервале [a, b] степениn, тогда

,

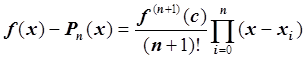где с – некоторая точка из отрезка [a, b].

Следствие

.

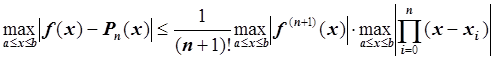Теперь, когда мы изложили некоторые сведения из математического анализа, возникает вопрос: как построить вычислительный алгоритм для нахождения значений интерполяционного полинома?

Переходим к рассмотрению вычислительного алгоритма построения интерполяционного полинома. Существует несколько вычислительных алгоритмов: полином Лагранжа, полином Ньютона, полином Стирлинга и другие. Мы подробно рассмотрим полином Лагранжа.

Важно понимать следующий факт: существует единственный полином степени n, который интерполирует n + 1 точку, но известны разные формы записи этого полинома, разные вычислительные алгоритмы для вычисления его значений.

5.5. Интерполяционный полином Лагранжа

Запишем интерполяционный полином в форме Лагранжа.

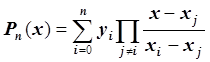,          где      .

В развернутом виде:

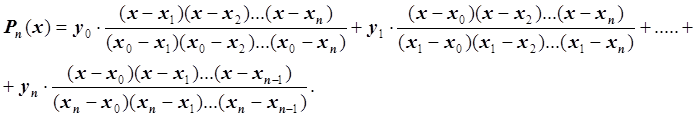
Сложность вычислительного алгоритма построения полинома Лагранжа

Число арифметических действий – ; объем памяти – .

5.6. Сходимость интерполяционных полиномов

Рассмотрим функцию  на отрезке  и последовательность интерполяционных полиномов   Возникает вопрос: существует ли для точки  предел этой последовательности и равен ли он значению: ?

Определение. Интерполяционный полином  сходится к функции  для  , если  .

Рассмотрим два примера.

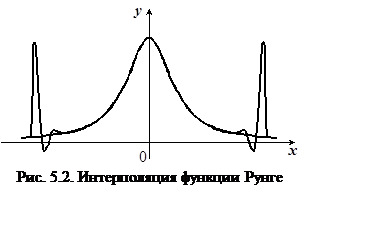
Пример 1 (Рунге)

В 1901 г. Рунге (1901 г.) рассмотрел интерполяцию полиномами на отрезке  функции 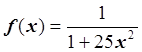   при равномерном распределении узлов сетки. Выяснилось, что при бесконечном увеличении степени n интерполяционного полинома , последовательность  расходится на интервале  (рис. 5.2). То есть

.

При этом  – достаточно «хорошая», гладкая функция.

Чем выше степень интерполяционного полинома, построенного по интерполяционной таблице с равномерным шагом для функции 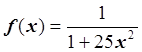, тем больше погрешность.