Итерационные методы решения систем нелинейных уравнений, страница 7

Если функция является непрерывно дифференцируемой на отрезке  [-1, 1], то интерполяционный полином , совпадающий с  в нулях полинома Чебышева степени n + 1, сходится к  при  для любой точки x из отрезка [-1, 1].

Практический вывод. Если интерполяция может выполняться с произвольным выбором узлов на отрезке [-1, 1], то целесообразно в качестве узлов выбрать нули полинома Чебышева.

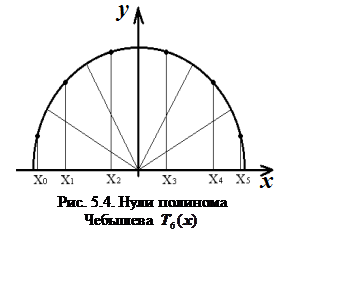
Геометрический смысл. Для отрезка [a, b] точки, соответствующие нулям полинома Чебышева на отрезке[-1, 1], получаются построением на отрезке [a, b] полукруга, делением этого полукруга на n равных  дуг и проецированием середин каждой из дуг на данный отрезок (рис. 5.4). Нули полинома Чебышева сгущаются к концам отрезка.

Кратко остановимся на главных моментах темы интерполяции полиномами.

Если в интерполяционной таблице все  различны ( при ), то существует единственный интерполяционный полином, степень которого на единицу меньше, чем размерность интерполяционной таблицы.

Известны разные формы записи одного и того же интерполяционного полинома (форма Лагранжа, форма Ньютона, форма Стирлинга).

Существует оптимальное распределение узлов интерполяции на отрезке [-1,1], а именно нули полинома Чебышева, использование которых для непрерывно дифференцируемых функций обеспечивает сходимость интерполяционных полиномов.

С ростом степени интерполяционного полинома требуется существование у  производных все более высокого порядка.

При неоптимальном распределении узлов интерполяции на отрезке [a, b] возможно увеличение погрешности с ростом степени интерполяционного полинома и возникновение осцилляции на концах отрезка.

Объем арифметических действий, необходимых для построения полинома Лагранжа – , полинома Ньютона  – . Объем памяти – .

5.8. Примеры решения задач

Задача 1

Проинтерполировать функцию  полиномом , причем совпадение значений  и  требуется при . Найти относительную погрешность приближения   значения.  

Решение

Прежде всего, построим интерполяционную таблицу:

.

x	0	1	2
y	1	2	4

Размерность таблицы равна: 3, ;

.

Получаем систему линейных уравнений:

                              

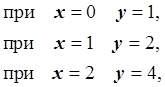
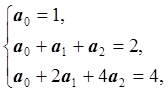
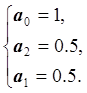
Получаем интерполяционный полином:

.

Проверим результат: ,         ,         ;

 – интерполяционный полином.

Найдём относительную погрешность:

,                         ,

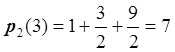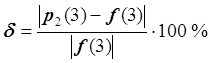f(3) = ,                                                 .

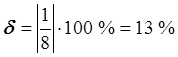Ответ: ,      .

Задача 2

Проинтерполировать функцию  функцией 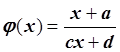 ,  причем совпадение значений  и  требуется при x = 0; 1; 2.  Найти относительную погрешность приближения  значения.

Решение

Построим интерполяционную таблицу:

x	0	1	2
y	1	2	4

Для нахождения неизвестных  составим систему уравнений:

                                     

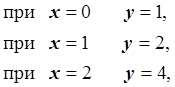
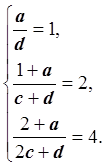
Полагая, что знаменатели дробей не обращаются в нуль, получаем систему линейных уравнений:

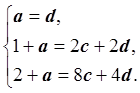
Система линейных уравнений имеет единственное решение:

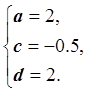
Следовательно, 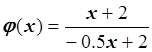         или      .

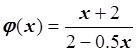Проверим результат:

,              ,               .

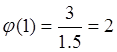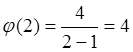Найдём относительную погрешность:

,             ,

.

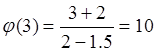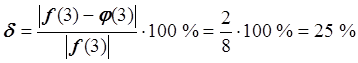Ответ: , .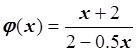

Отметим, что функция 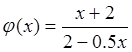 не является непрерывной при x = 4. В отличие от задачи 1 задача 2 не всегда имеет решение. Существуют интерполяционные таблицы, для которых нельзя построить интерполяционную функцию j(x). В этом случае в ответе нужно указать, что задача не имеет решения.

Задача 3

По интерполяционной таблице построить интерполяционный полином   и представить его в виде суммы полиномов Чебышева. Указать число M такое, что

  для :

x	-1	0	1
y	6	1	2