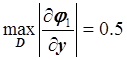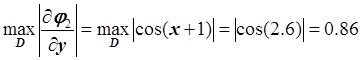Итерационные методы решения систем нелинейных уравнений, страница 4

,            ;

М₁₁ = 0,             М₁₂ = 0.5,       М₂₁ = 0.86,     М₂₂ = 0;

,         .

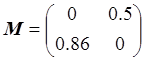, метод итераций сходится для любого вектора начального приближения  из области D.

2. Выберем вектор начального приближения:  =  (1.,0.).

3. Формулы метода итераций:

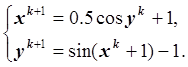
4. Условие остановки итерационного процесса:

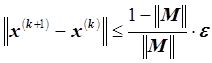,                   ||M|| = 0.86.

Вектор , для которого выполняется условие остановки итерационного процесса, является приближенным решения системы нелинейных уравнений, полученным методом итераций с точностью e.

Задача 3

Известно, что область D = { – 5 £ x £ 5, – 5 £ y £ 5} содержит одно решение системы нелинейных уравнений:

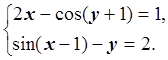
Обосновать применение метода Ньютона для уточнения решения.

Решение

В данной задаче требуется проверить условия для функций f₁ , f₂ ,  а именно:

1) функции являются дважды непрерывно дифференцируемыми в области D;

2) якобиан не равен нулю в области D.

В нашем случае:  .

Функции являются дважды непрерывно дифференцируемыми в области D. Вычислим элементы матрицы Якоби:

,             ,         ,        .

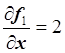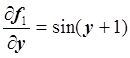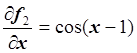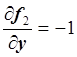Запишем матрицу Якоби:

.

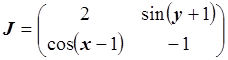Вычислим якобиан:  . Якобиан не равен нулю в области D, так как произведение функций  и  при любых значениях аргумента по модулю ограничено единицей ,  .

Таким  образом,  произведение этих двух функций не может принимать значение –2. Следовательно, определитель матрицы Якоби не обращается в ноль в области D. Таким образом, выполнены все условия на применение метода  Ньютона в области D для уточнения решения.

Задача 4

Известно, что решение системы нелинейных уравнений:

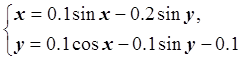       ( где    измеряются в радианах)

принадлежит области . Построить и обосновать алгоритм  решения систем нелинейных уравнений методом итераций с точностью .

Решение

Область D – квадрат, следовательно, D – выпуклая область, содержащая одно решение системы нелинейных уравнений. Система уже приведена к виду, удобному для итераций:

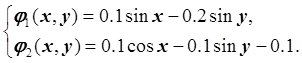
1. Функции непрерывно дифференцируемы в области D. Найдем элементы матрицы М и вычислим  :

       ,      ,     .

,                         ;

,                                    ;

,                       .

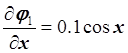
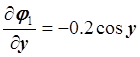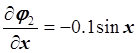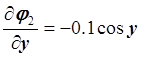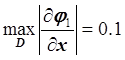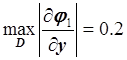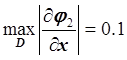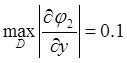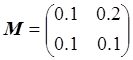, метод итераций сходится для любого начального приближения  из области D.

2. Начальное приближение: .

3. Формулы метода:

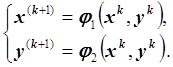
Так как , то последовательность  сходится к точному решению системы нелинейных уравнений.

4. Условие остановки итерационного процесса:

,        .

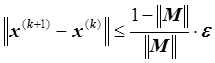Вектор , удовлетворяющий условию остановки итерационного процесса, является приближенным решением, полученным методом итераций с точностью e.

5. Интерполяция полиномами

5.1. Интерполяционная таблица

Определение. Рассмотрим отрезок  и конечное множество, состоящее из точек , удовлетворяющих следующему условию:

.

Множество точек  называется сеткой на отрезке .

Сетка – это одно из основных понятий. Точки ,    называются узлами сетки. В дальнейшем мы будем рассматривать только такие сетки, в которых все узлы сетки различны ( для ) и упорядочены по возрастанию.

Определение. Пусть заданы вещественные числа . Таблица, состоящая из значений ,  ,  называется интерполяционной таблицей, где  – узлы сетки,  – значения некоторой функции в узлах сетки.

Пример

x	-1	0	1
y	1	0	1

Часто рассматриваются сетки с равномерным распределением узлов:  (равномерные сетки).

Как правило, числа  интерпретируются как значения некоторой функции . При этом  может быть задана аналитически (формулой) или только своими значениями, например, полученными в результате измерений. Рассмотренный нами пример интерполяционной таблицы можно интерпретировать как таблицу значений  на отрезке [-1, 1].

Рекомендуемая литература: /1-4, 7-10, 12, 13/.