Мы получили систему линейных уравнений. Эта система линейных уравнений решается методом Гаусса с частичным выбором ведущего элемента.
3. Выбираем точку начального приближения: ![]() .
.
4. Условие остановки итерационного процесса:
![]() .
.
Для первой нормы вектора условие остановки итерационного процесса запишется в виде:
![]() .
.
Вектор ![]() , для которого выполняется
условие остановки итерационного процесса, является приближенным решением, полученным методом Ньютона.
, для которого выполняется
условие остановки итерационного процесса, является приближенным решением, полученным методом Ньютона.
Недостатки метода Ньютона
1. Для применения метода Ньютона необходимо близкое к точному решению начальное приближение. Если начальное приближение задано грубо, то метод может разойтись или привести к другому решению.
2. На каждом шаге k
итерационного процесса необходимо решать систему линейных уравнений или
находить обратную матрицу, а это требует O(![]() ) арифметических действий для
каждого k.
) арифметических действий для
каждого k.
Пусть известна выпуклая область D, содержащая одно решение системы нелинейных уравнений
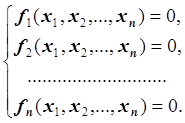
или в векторном виде: ![]() ,
, ![]() ,
, ![]()
Запишем эту систему в виде:
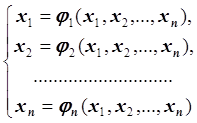 или
в векторном виде:
или
в векторном виде: ![]() , где
, где ![]() ,
, ![]() .
.
Системы ![]() и
и ![]() эквивалентны.
эквивалентны.
Пусть функции ![]() являются непрерывно
дифференцируемыми в области D.
Запишем формулы метода итераций:
являются непрерывно
дифференцируемыми в области D.
Запишем формулы метода итераций:
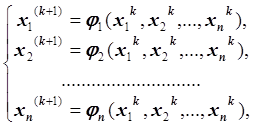
где ![]() – номер
итерации.
– номер
итерации.
Таким образом, строим последовательность векторов ![]() , начиная с некоторого вектора приближения
, начиная с некоторого вектора приближения ![]() . Естественно, возникают следующие вопросы:
при каких условиях последовательность
. Естественно, возникают следующие вопросы:
при каких условиях последовательность ![]() сходится
к вектору точного решения с и как выбирается вектор начального
приближения
сходится
к вектору точного решения с и как выбирается вектор начального
приближения ![]() ?
?
Теорема (о сходимости)
Если функции ![]() являются непрерывно дифференцируемыми в
выпуклой области D, содержащей одно решение системы
являются непрерывно дифференцируемыми в
выпуклой области D, содержащей одно решение системы ![]() , то для сходимости метода
итераций достаточно, чтобы хотя бы одна из норм матрицы M была меньше 1, где элементы матрицы находятся по формуле:
, то для сходимости метода
итераций достаточно, чтобы хотя бы одна из норм матрицы M была меньше 1, где элементы матрицы находятся по формуле:
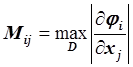 .
.
В качестве начального приближения в этом случае можно взять любую точку из области D.
Оценка погрешности. При выполнении условий теоремы о сходимости справедливо
следующее неравенство: 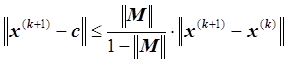 .
.
Следовательно, условие остановки итерационного процесса записывается следующим образом:
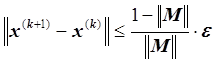 .
.
Вектор ![]() , для которого выполняется условие
остановки итерационного процесса, является приближенным решением,
полученным методом итераций с точностью
, для которого выполняется условие
остановки итерационного процесса, является приближенным решением,
полученным методом итераций с точностью ![]() .
.
Алгоритм метода итераций
1. Находим выпуклую область D, содержащую одно решение системы нелинейных
уравнений ![]() . Записываем систему нелинейных уравнений в
виде
. Записываем систему нелинейных уравнений в
виде ![]() , причем эти две системы должны быть
эквивалентны:
, причем эти две системы должны быть
эквивалентны:
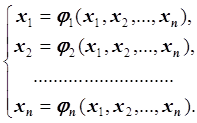
Кроме этого, ![]() должны быть непрерывно дифференцируемыми в
D и хотя бы одна из норм матрицы M должна быть меньше единицы, где
элементы матрицы M находятся по
формуле:
должны быть непрерывно дифференцируемыми в
D и хотя бы одна из норм матрицы M должна быть меньше единицы, где
элементы матрицы M находятся по
формуле: 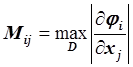 .
.
2. Выбираем начальное приближение: ![]() –
произвольную точку из D.
–
произвольную точку из D.
3. Строим итерационный процесс:

Последовательность ![]() сходится
к точному решению c, так как
сходится
к точному решению c, так как ![]() .
.
4. Условие остановки итерационного процесса: 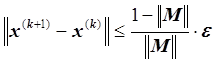 .
.
Вектор ![]() , для которого выполняется условие
остановки итерационного процесса, является приближенным решением,
полученным методом итераций с точностью e.
, для которого выполняется условие
остановки итерационного процесса, является приближенным решением,
полученным методом итераций с точностью e.
Таким образом, ![]() .
.
Пример 1
Построить
алгоритм решения системы нелинейных уравнений методом итераций с точностью ![]() :
:
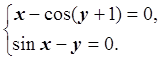
Решение
Мы уже отделяли область ![]() ,
содержащую одно решение этой системы нелинейных уравнений. D – выпуклая область.
,
содержащую одно решение этой системы нелинейных уравнений. D – выпуклая область.
1. Запишем систему в виде:
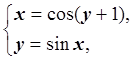
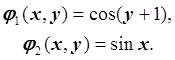
Функции ![]() непрерывно
дифференцируемы в D.
непрерывно
дифференцируемы в D.
Вычислим:
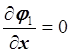 ,
, 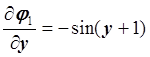 ,
,
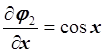 ,
, 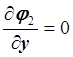 .
.
Построим матрицу M:
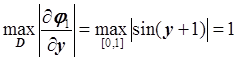 ,
,
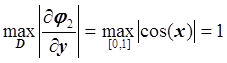 , следовательно,
, следовательно, ![]() .
.
Необходимо уменьшить область D таким образом, чтобы эта область
содержала решение и ![]() ,
, ![]() .
.
Рассмотрим прямоугольник: ![]() .
.
D – выпуклая область, содержащая одно решение системы нелинейных уравнений.
Вычислим ![]() и докажем, что
и докажем, что ![]() :
:
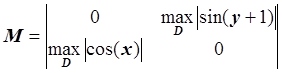 ,
, 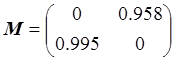 ;
;
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.