Государственный комитет РФ по высшему образованию
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Санкт-Петербург
1995
![]()
Гармонический анализ периодических импульсных последовательностей.
I.I. Основные теоретические положения и расчетные формулы
Периодическое колебание U(t), например, последовательность прямоугольных импульсов с периодом Т (рис.1.1) может быть представлено рядом Фурье как сумма гармонических составляющих с частотами, кратными "основной" частоте этого колебания:
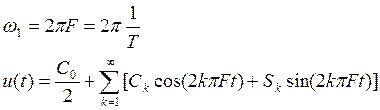 (1.1)
(1.1)
где: К = 1,2.3... - коэффициент
кратности, 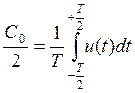 - среднее значение колебания u(t) за период Т, а коэффициенты Ск и Sк определяются интегрированием u(t) с весовыми гармоническими функциями кратной
частоты в пределах периода Т(интервала ортогональности):
- среднее значение колебания u(t) за период Т, а коэффициенты Ск и Sк определяются интегрированием u(t) с весовыми гармоническими функциями кратной
частоты в пределах периода Т(интервала ортогональности):
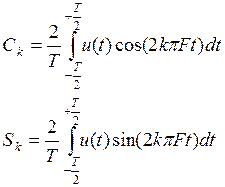 (1.2)
(1.2)
При практическом вычислении интегралов (1.2) следует учитывать, что выбор "начала отсчета" t = 0 на рис.1.1 для периодического сигнала является произвольным. При удачном выборе точки t=0 в используемой системе координат иногда возможно значительное сокращение вычислений. Так, на рис.1.2 начало отсчета t = 0 совмещено с серединой импульса в последовательности u(t). Тогда подынтегральные выражения в (1.2) приобретают четный и нечетный характер соответственно, следовательно, все коэффициентыSк=0, а величиныСк можно вычислить по формуле:
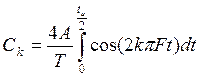 (1.3), где интегрирование
прямоугольного импульса с амплитудой A=const обеспечивается соответствующим
выбором пределов интеграла.
(1.3), где интегрирование
прямоугольного импульса с амплитудой A=const обеспечивается соответствующим
выбором пределов интеграла.
Для сопоставления с результатами эксперимента ряд Фурье (1.1) удобно представить в форме:
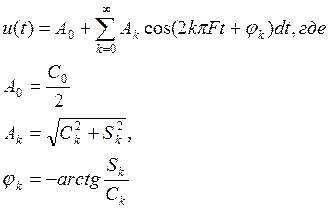 (1.4), (1.5)
(1.4), (1.5)
(обратите внимание на знак минус!!!)
Для прямоугольного импульса результаты вычисления по (1.3) дают:
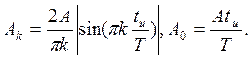
Экспериментальный анализ состоит в выделении из колебания гармонических составляющих (I.4) с помощью колебательного контура, настроенного на соответствующую частоту, и измерении амплитудAк и фазjк этих гармоник. Совокупность {Aк} называется амплитудным, {jк}- фазовым спектром колебанияu(t).
В лабораторной работе измерение Aк и jк осуществляется по диаграмме гармоники, наблюдаемой на экране электронного осциллографа. На рис.1.3 представлен пример такой диаграммы для второй гармоники входной последовательности импульсов. Номер гармоники К=2 можно определить сопоставлением периода Т - основной частоты и периода Т2=T/2 данной гармоники. Для удобства измерений на диаграмме рис.1.3 предусмотрены специальные метки, соответствующие переднему и заднему фронтам импульсов входной последовательности u(t) .
АмплитудаAк любой гармоники определяется по амплитудной шкале электронного осциллографа безотносительно к временной шкале.
В то же время измерение фазы jк гармонической составляющей
![]() (1.6)
(1.6)
непосредственно определяется привязкой временной шкалы. Определить jк можно из условия максимума мгновенного значения uk(t) гармоники. Согласно (I.6) имеем (с точностью до 2p):
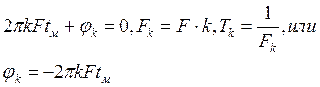 (1.7)
(1.7)
Таким образом фаза связана с отсчетом времени tм, соответствующим максимуму гармоники, а величина tм определяется в системе координат с произвольно выбираемым началом отсчета t=0 . Поэтому, если использовать систему отсчета рис.1.2, то tм может принимать значения либо 0, либо T/2 . Из диаграммы рис.1.3 определяем tм = 0 и согласно (1.7) имеем j2 = 0. Однако, если для этого же колебания использовать систему координат рис. 1.1 (что представлено пунктирной осью на рис 1.3) то получаем tм и согласно (1.7) имеем:
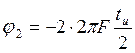 (1.8)
(1.8)
Связь изменения величины фазы с изменением отсчета временной шкалы является общим свойством фазовых измерений. При этом наиболее характерно, что согласно (I.7) величина фазы является линейной функцией от произведения временного положенияtм и частоты гармоники (номера К).
Ясно, что аналогичные изменения
в фазовом спектре колебания происходят и вследствие изменения временного
положения (запаздывания или опережения) анализируемого колебания в условиях, когда
шкала отсчета времени выбрана и неизменна. Появление линейно зависящего от
частоты фазового слагаемого спектра ![]() вследствие задержки сигнала на
время tз является одним из основных
свойств преобразования Фурье.
вследствие задержки сигнала на
время tз является одним из основных
свойств преобразования Фурье.
1.2. Описание экспериментальной установки для гармонического анализа.
Для проведения измерений используется аппаратура согласно структурной схеме рис.1.4. В качестве, генератора импульсов используется прибор Г5-54, дающий последовательность прямоугольных импульсов с соответствующими заданию на работу параметрами
F - частота повторения, tи - длительность импульса, А - его амплитуда (см. рис.1.1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.