Методические указания к лабораторным работам № 1-6 по дисциплине "Радиотехнические цепи и сигналы" (Гармонический анализ периодических импульсных последовательностей. Исследование преобразования гармонического колебания нелинейным элементом с кусочно-линейной амплитудной характеристикой), страница 8

Тогда диаграмму выходного напряжения можно просто построить как разность переходных характеристик, сдвинутых на интервал t_и .

На рис. 5.2. такое построение проведено для цепочки интегрирующего типа, переходная характеристика которой исследована в лабораторной работе №4 (рис.4.1.),

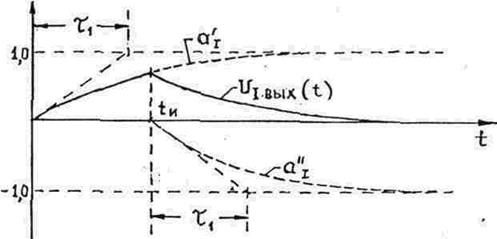
Рис.5.2

Аналитически выходное напряжение определяется согласно с (5.1) различными выражениями на различных интервалах времени:

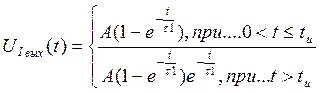                (5.2)

Из этих соотношений и интеграла (5.1) видно, что если длительность входного импульса много меньше постоянной времени цепи, то выходное напряжение  U_вых(t) в каждый момент времени совпадает с импульсной характеристикой цепи  h (t) .

В другой предельной ситуации, когда длительность сигнала U_вх(t) много больше длительности импульсной характеристики, выражение (5.1) определяет выходное напряжение цепи как интеграл от импульсной характеристики, т.е. U_вых(t) совпадает с переходной характеристикой. Эти соображения обосновывают способы измерения импульсных и переходных характеристик, использованные в лабораторной работе №4.

В общем случае, когда длительность входного сигнала сопоставима с постоянной времени цепи, т.е. длительностью её импульсной характеристики, форма сигнала на выходе цепи существенно отличается от формы входного сигнала.

Заметим, что вычисления U_вых(t) по (5.1) требуют числа умножений, пропорционального квадрату размерности массивов представления U_вх(t) и h(t) , что ограничивает применение временных методов областью относительно коротких сигналов.

5.2. Описание экспериментальной установки.

Для проведения измерений используется экспериментальная установка, состоящая из измерительного генератора периодических импульсных сигналов,  линейных  радиотехнических  цепей  рис  2.1.а,б,в (лабораторная  работа  №2)  и  электронного  осциллографа для наблюдения процессов на входах и выходах цепей.

5.3. РАСЧЕТНАЯ ЧАСТЬ

При подготовке  к  работе  следует  построить  выходные  напряжения цепочек   рис. 2.1.а, б, в   для  длительности  входного  импульса t_и, использованной  в  лабораторной  работе  №1  в  соответствии  с  номером рабочего  места.  При  построении использовать переходные характеристики рис.4.1.,4.2.,4.3., --  результаты  лабораторной  работы  №4.   Диаграммы напряжений построить с соблюдением масштабов осей времени и напряжения.

5.4. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

При выполнении   работы   произвести  осциллографические  измерения рассчитанных напряжений и представить результаты в  системах  координат, совместных  с  расчетными.  Для  каждой  цепи  изменить  в  1.5-2 раза длительность импульса в  большую  сторону  и  меньшую  сторону  а  также зарисовать   диаграммы   выходного   напряжения.   Объяснить  полученные результаты.  Сравнить   их   с   результатами   гармонического   анализа (лабораторные работы №1,2,3)

5.5. СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать:

- структурную схему экспериментальной установки;

- расчеты выходных напряжений RC-цепи; графики;

- осциллограммы выходных напряжений;

- выводы по работе.

5.6. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какими   методами   рассчитываются, выходные  сигналы  линейных радиотехнических цепей?

2. Какой  зависимостью  во  временной  области  связаны  входной  и выходной сигналы линейной радиотехнической цепи?

3. Описать   порядок   расчёта   выходного  сигнала  линейной  цепи временным методом.

4. Почему     при    вычислении    выходного    сигнала    реальной радиотехнической цепи свертка  вычисляется  только  для  неотрицательных времен?

5. В чем особенность расчета выходного  сигнала  временным  методом при входном воздействии в виде прямоугольного импульса?

6. Сколько существует интегралов свёртки во временной области. Уметь привести и вывести, по крайней мере, четыре.

Лабораторная  работа № 6.

Исследование преобразования гармонического колебания нелинейным элементом с кусочно-линейной амплитудной характеристикой.

6.1. Основные теоретические положения и расчетные формулы.

При воздействии синусоидального колебания с постоянной составляющей Е_о

U_вх(t)=U_м·cos(2pF_ot)+E_o(6.1)

Ha безынерционный нелинейный элемент, амплитудная характеристика которого допускает кусочно-линейную аппроксимацию:

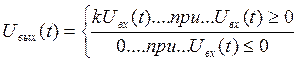        (6.2)