Методические указания к лабораторным работам № 1-6 по дисциплине "Радиотехнические цепи и сигналы" (Гармонический анализ периодических импульсных последовательностей. Исследование преобразования гармонического колебания нелинейным элементом с кусочно-линейной амплитудной характеристикой), страница 6

Во временной области характеристиками линейных радиотехнических цепей являются их отклики на специальные тестовые воздействия. Наиболее распространены переходные и импульсные характеристики.

4.1.1. Переходной характеристикой  а(t) называется отклик цепи на тестовое воздействие в виде функции включения (единичного скачка) - б(t). Для расчета переходной характеристики методом Лапласа следует найти изображение выходного напряжения цепи как произведение передаточной функции   Н(р) цепи и изображения единичного скачка:

А(р)=Н(р)   (4.1)

Обратное преобразование Лапласа от (4.1) дает переходную характеристику

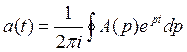
и может быть найдено с помощью теоремы о вычетах функции A(p). Однако, для простейших цепей типа рис.2.1 (лабораторная работа №2) целесообразно использовать непосредственное построение переходного процесса на основе законов электротехники. Так, для цепи рис.2.1.а переходный процесс состоит в заряде конденсатора  C₁ с постоянной времени t₁ от нулевого значения в момент  t=0   до асимптотического уровня 1 при tॠ. Построение переходной характеристики в этом случае иллюстрируется на рис.4.1

			Рис. 4.1
				б)

 

Рис.4.1

В качестве параметра переходной характеристики

a_I =(1-e^-t/t)  б(t)         (4.2)

обычно используют длительность нарастания напряжения до уровня 0,9 от асимптотического (длительность фронта переходной характеристики t_фp). Логарифмируя (4.2) легко найти   t_фр=2,3 t₁ .Из рис.4.1. следует, что переходная характеристика (4.2) представляет результат интегрирования единичного скачка б(t) ,. т.е. линейно – возрастающую функцию лишь для малых интервалов времени  t<< t₁ , т.е. операция интегрирования с помощью цепи рис.2.1.а осуществляется лишь приближенно. Этот вывод полезно сравнить с частотным описанием свойств "интегрирующей" цепи в лабораторной работе №2.

Переходная характеристика "дифференцирующей" цепи (рис.2.7.б)

а_D = e^-t/t2  б(t)         

изображена на рис.4.2. .Здесь заряд конденсатора С₂  выражается в уменьшении выходного напряжения цепи с постоянной времени t₂

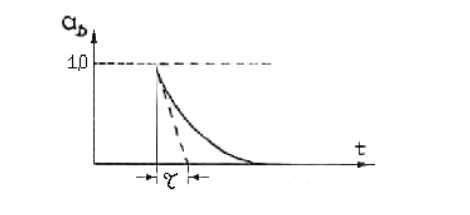
Рис.4.2.

Ясно, что эта функция описывает операцию дифференцирования единичного скачка также лишь приближенно.

Переходная характеристика моста Вина выражается суммой двух экспонент и приближенно может быть построена как на рис.4.3.

при R₃=R₄=R, C₃=C₄=C, t=RC

a(t)

            При экспериментальном измерении возникает ряд особенностей по сравнению с рассмотренной идеализированной схемой, поскольку используется не идеальный единичный скачок, а периодическая последовательность импульсов, что обеспечивает возможность наблюдения процессов на экране электронного осциллографа. Используемые импульсы имеют конечную длительность  t_и  и конечное время нарастания/спада t_фр, как показано на рис.4.1.а пунктиром. Из этих диаграмм следует, что для точного измерения переходной характеристики эти параметры следует выбирать из условий:

.

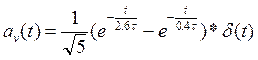
t_фр << t _{1   ,}   t_и>> t ₁           (4.3)

При этом следует учитывать, что спад испытательного импульса при t³t_и  вызывает в исследуемой цепи переходный процесс, являющийся переходной характеристикой с обратной полярностью.

Наконец, периодическая последовательность импульсов длительностью t_и , амплитудой     А  и с периодом  Т   имеет в своем спектральном составе (cм.(I.4)  в лабораторной работе №1) постоянное слагаемое

А_о=A t_и / T    (4.4)

До этой величины напряжения постоянного тока заряжаются конденсаторы C1,C2,C3 в цепочках рис.2.1, что приводит к смещению уровня ноля на экране осциллографа. Уменьшения этого явления можно достичь, увеличивая период испытательных импульсов до величины: Т>> t_и.    (4.5)

4.1.2. Вторым видом временных характеристик линейных радиотехнических цепей являются импульсные характеристики. Импульсной характеристикой  h(t)  называется отклик цепи на входное воздействие в виде d-функции d(t) . Поскольку формально d(t)  является производной от единичного скачка: