Методические указания к лабораторным работам № 1-6 по дисциплине "Радиотехнические цепи и сигналы" (Гармонический анализ периодических импульсных последовательностей. Исследование преобразования гармонического колебания нелинейным элементом с кусочно-линейной амплитудной характеристикой), страница 4

Полагая здесь p=iw , определяют передаточную характеристику:

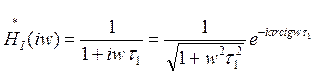                  (2.4)

Аналогично для цепи рис.2.1.б можно найти:

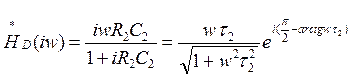     (2.5)

Для цепи второго порядка (мост Вина, рис.2.1.в) получается более сложное выражение, которое можно упростить, положив R₃=R₄, С₃=С₄ иRC=t тогда

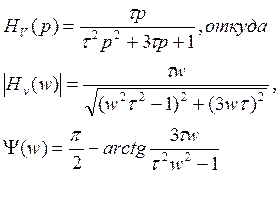(2.6)

Модуль частотной характеристики имеет экстремум (максимум) при частоте w_о=1/t , при этом Н_max(w)=1/3 и Y_w=w0=0. Значения аргументов w_гр=2pf_гр при которых амплитудно - частотная характеристика уменьшается до 0,707 от максимума называются граничными частотами.

При анализе частотных характеристик цепей всегда полезно  рассматривать предельные значения частоты:w=0, wà ¥ . Например, для цепи рис.2.1.а из (2.4) при wt>>1 получаем

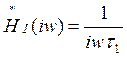
что в соответствии со свойствами преобразования Фурье является математически строгим выражением операции интегрирования и определяет использование для данной цепочки названия "интегрирующая". В то же время при wt₁<<1 эта цепочка не оказывает никакого влияния на сигнал  Н_I(iw)=1 .

Цепочка рис. 2.1.б на таких же основаниях называется "дифференцирующей", что реализуется при wt₂<<1  ; тогда

а при wt₂>>1  имеем     H_D(iw)=1.

Наконец, наличие экстремума частотной характеристики моста Вина (рис.2.1.в) объясняется не пропусканием низких частотwt<<1цепочкой С₃R₃, и шунтированием высоких частот wt >>1   цепочкой C₄R₄ .

2.2. Описание экспериментальной установки для измерения частотных характеристик цепей.

Для экспериментального измерения амплитудно-частотной характеристики в лабораторной работе используется измерительный генератор синусоидальных сигналов, напряжение с выхода которого подается на вход исследуемой цепи, а амплитуда выходного напряжения цепи измеряется по экрану осциллографа в требуемом диапазоне частоты  f.

ОСЦИЛЛОГРАФ

Для измерения фазо-частотной характеристики электронный осциллограф включается в режим наблюдения фигур Лиссажу. Для этого, как показано на рис.2.3., напряжение измерительного генератора подается на вход исследуемой цепи и на горизонтально - отклоняющие пластины осциллографа (Вход "X"). Напряжение с выхода цепи подается, как обычно, на вертикально - отклоняющие пластины "У".

 

Рис.2.3.

При этом на экране осциллографа наблюдается эллипс с параметрами, показанными на рис.2.4.

.

Рис.2.4.

Для гармонических колебаний на входе и выходе цепи:

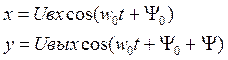
из условия у=0 получаем:

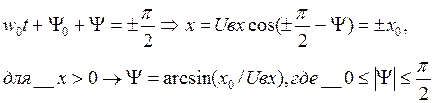 (2.7)

Определяя по  диаграммам  рис.2.4  параметрыx_o ,U_вх   по   (2.7) рассчитывают  фазочастотную  характеристику.  Заметим,  что  при | Y|<π/2 эллипс располагается в I и III четвертях, а знак определяет направление движения луча на экранеи, к сожалению, визуально неразличим.

2.3. РАСЧЕТНАЯ ЧАСТЬ

1. Рассчитать  амплитудно-частотные и фазочастотные характеристики для цепей рис.2.1. при заданных параметрах:

R₁ = 3,3 кОм, С₁ = 72nF, R₂ = 3,0 к0м, С₂=33nF, R₃=R₄=2к0м, С₃=С₄=72nF.

2. Рассчитать  постоянные  времени и граничные частоты f_rp цепочек. Оценить  требуемый  диапазон  изменения  частоты  f  в  каждом   случае. Построить рассчитанные характеристики (2.1) в виде диаграмм H(f)  и Y (f).

2.4. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Для проведения  эксперимента  по  снятию  АЧХ  и ФЧХ линейных цепей необходимо собрать схему согласно рис.2.3. Установить на входе амплитуду колебаний, равную 2В и поддерживать ее постоянной во время эксперимента. Изменяя частоту гармонических колебаний на  входе  и  измеряя  амплитуду колебаний   на  выходе  цепи,  найти  значения  АЧХ  на  соответствующих частотах.

Измерение ФЧХ  осуществляется  по  фигурам Лиссажу,  наблюдаемым на экране осциллографа.

2.5. СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать:

- структурную схему экспериментальной установки;

- расчеты  АЧХ  и  ФЧХ  для  трех  видов  RC-цепей,   сведенные   в таблицу; графики;

- экспериментальные  данные,  сведенные в таблицу;  графики АЧХ и ФЧХ совмещенные с расчетными графиками;

- выводы по работе.

2.6. КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Что  такое  линейная радиотехническая цепь с постоянными параметрами? Какие ещё бывают цепи, и чем они различаются?