jк = -2p *1/L (1.9),
где l – это tм, L – 1/(k*F), p = 180О
Для расчета по формуле (1.9) величины 1 и L могут быть измерены по экрану осциллографа в единицах времени в соответствии с масштабом используемой шкалы или просто в единицах длины (числе клеток экрана).
Измерение фаз произвести дважды: а) для начала отсчета, совпадающего с серединой входного импульса;
б) для начала отсчета, совпадающего с передним фронтом импульса.
Результаты измерений спектров представить в общей системе координат с результатами расчетов. Результаты этой работы необходимо хранить для выполнения последующих работ.
При изображении фазового спектра иметь ввиду, что на фазовых диаграммах вследствие периодичности этого параметра возможны "скачки" фазы на величину ± p.
Диаграммы гармоник с номерами К=1,2,3 следует зарисовать в системе координат, совмещенной по времени с диаграммами входных импульсов.
Сделать выводы по работе.
1.5. СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать:
- структурную схему экспериментальной установки;
- расчеты амплитудного и фазового спектров (начало отсчета совпадает с серединой импульса и передним фронтом импульса), сведенные в таблицу;
- графики;
- экспериментальные данные, сведенные в таблицу;
- графики, совмещенные с расчетными;
- выводы по работе.
1.6. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое спектр сигнала (амплитудный, фазовый, энергетический), спектральная плотность?
2. Почему при описании сигнала используют системы ортогональных базисных функций?
3. Что такое тригонометрический ряд Фурье, какие сигналы могут быть представленны рядом Фурье?
4. Как определяются коэффициенты тригонометрического ряда Фурье?
5. Как отразится на спектре периодической последовательности прямоугольных импульсов изменение длительности импульса и периода повторения?
6. Как связаны спектр периодического и спектральная плотность одиночного импульса одинаковой формы?
7. Как изменится спектр периодического сигнала, если длительность импульса устремить к нулю?
8. Как изменится спектр сигнала, если период повторения устремить в бесконечность?
9. Как влияет на амплитудный и фазовый спектры сигнала изменение отсчета времени?
10. Как зависит ширина спектра сигнала от длительности импульса?
11. Что такое фаза?
 |
Частотные характеристики линейных радиотехнических цепей с постоянными параметрами.
2.1. Основные теоретические сведения и расчетные формулы.
Для представления характеристик линейных цепей в частотной области используется комплексная передаточная характеристика
![]() (2.1)
(2.1)
модуль Н(f) и фаза Y(f) которой называются амплитудно-частотной и фазо-частотной характеристиками и определяют отношение амплитуд и разность фаз гармонических сигналов частоты f на выходе и входе цепи.
Для расчета Н(iw) удобно использовать отношение изображений по Лапласу выходного Uвых(р) и входного Uвх (p) сигналов:
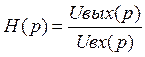 ,
(2.2)
,
(2.2)
которое определяет передаточную характеристику (2.1) на мнимой оси плоскости р=(iw).
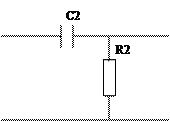
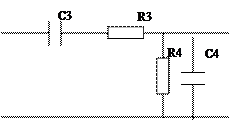
В лабораторной работе исследуются широко распространенные RC - цепочки первого и второго порядков (рис.2.1 а,б,в).
 |
|||||||||||||
 |
 |
||||||||||||
|
|
|
|||||||||||
Рис.2.1.
Расчет передаточных характеристик этих цепочек можно выполнить по обобщенной схеме рис.2.2.
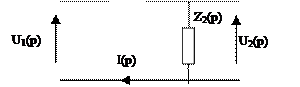 |
|||
Рис.2.2.
В соответствии с правилами Кирхгофа для этой цепочки имеем:
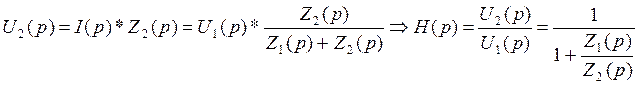 (2.3)
(2.3)
Естественно, что передаточная характеристика цепи Н(р) не зависит от вида входного сигнала и его изображения, U1(р) , хотя, как отмечалось, амплитудно- частотная H(f) и фазо-частотная Y(f) характеристики в (2.1) могут рассматриваться как результаты измерения амплитуды и фазы гармонического сигнала частоты f .
Для цепочки рис.2.1.а:
и с помощью (2.3) легко получить
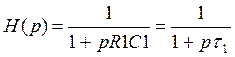
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.