Сборник задач по дисциплине "Теоретическая механика". Часть 1 (Условия 28 задач и решение задач № 1-20)

2. Условия задач

1.  Точки А и В движутся в плоскости рисунка (рис. 2.1): точка А – по прямой, а точка В – преследует точку А (ее скорость направлена на текущее положение точки А). . Начальное положение точек  и  отстоят на расстояние . Найти путь, пройденный точкой А до встречи с точкой В. (9 баллов)

2. 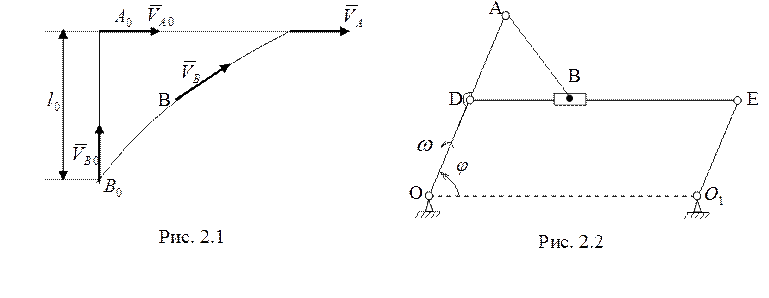 Стержень ОА шарнирного параллелепипеда (рис. 2.2) вращается с угловой скоростью . Расстояния . Найти скорость и ускорение ползуна В в тот момент времени, когда угол .      (4 балла)

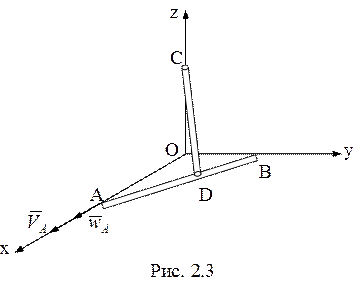
3.  Стержни АВ и CD одинаковой длины  соединены шарнирно в точке D (рис. 2.3). Точки А, В, С скользят вдоль осей Ox, Oy, Oz соответственно. . В указанном положении скорость и ускорение точки А , угол . Для этого момента времени найти скорость и ускорение точки С и угловую скорость стержня CD, пренебрегая ее составляющей вдоль оси стержня. (7 баллов)

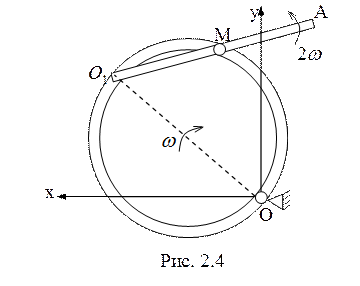
4.  Кольцеобразный желоб радиуса  равномерно вращается вокруг оси, проходящей через шарнир О и перпендикулярной плоскости желоба, с угловой скоростью  (рис. 2.4). Стержень  равномерно вращается в этой плоскости вокруг точки , связанной с желобом, в противоположную сторону с угловой скоростью  относительно желоба. Точки О и  лежат на одном диаметре. Штифт М скользит в прорези желоба и стержня одновременно. В начальный момент времени прямые  и  совпадали. Найти в зависимости от времени скорость и ускорение штифта и модули этих величин при малых углах поворота кольца. Толщиной желоба и стержня пренебречь. (6 баллов)

5.   Механизм совершает движение в плоскости рис. 2.5. Стержень ОВ вращается с постоянной угловой скоростью , расстояния , . Для данного положения, когда ОВ перпендикулярен ОА, найти скорость и ускорение ползуна С. (6 баллов)

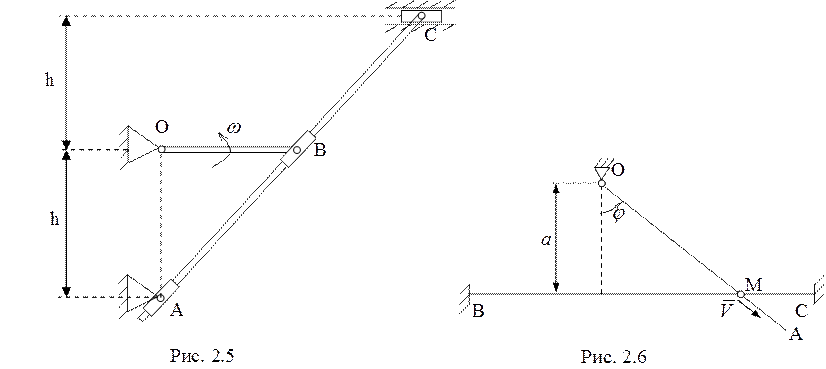
6.  Кольцо М одето одновременно на неподвижный стержень ВС и подвижный стержень ОА (рис. 2.6), вращающийся в плоскости рисунка вокруг оси, удаленной на расстояние  от прямой ВС. Скорость кольца относительно стержня ОА . Определить абсолютное кольца и угловое ускорение стержня ОА при угле . (6 баллов)

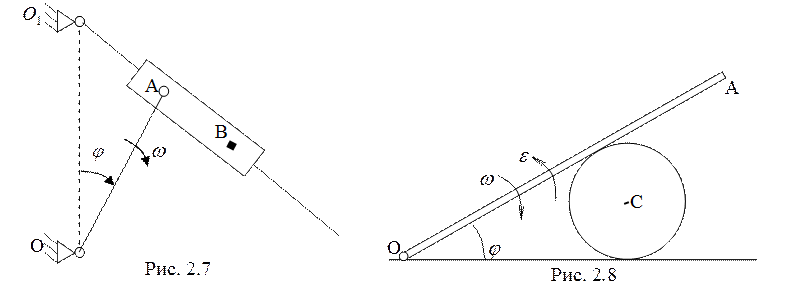
7.  Стержень ОА равномерно вращается в плоскости рис. 2.7 в указанном направлении с угловой скоростью . В положении, определяемом углом , найти скорость и ускорение точки В кулисного камня, если . (4 балла)

8.  Стержень ОА замедленно вращается в плоскости рис. 2.8 вокруг точки О с угловой скоростью  и угловым ускорением , выталкивая диск радиуса , движущийся в этой же плоскости. Найти скорость и ускорение центра диска в зависимости от угла . (2 балла)

9. 

Стержень АВ длины  скользит своими концами по экватору и меридиану сферы радиуса  (рис. 2.9). Скорость точки А равна  и постоянна. Найти скорость и ускорение точки В при угле .(6 баллов)

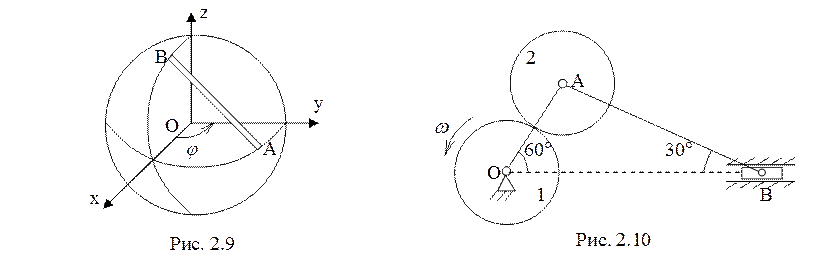
10. На неподвижную ось О свободно насажены зубчатое колесо 1 радиуса  и стержень ОА длины , не связанные между собой (рис. 2.10). С шатуном АВ жестко скреплено зубчатое колесо 2. Колесо 1 равномерно вращается с угловой скоростью  и, захватывая зубья колеса 2, приводит в движение шатун АВ и стержень ОА. Для показанного на рисунке положения механизма найти скорость и ускорение ползуна В. (10 баллов)

11. Механизм, состоящий из трех шарнирно соединенных стержней и ползуна (рис. 2.11), движется в плоскости своего расположения так, что скорости точек A и D равны по модулю , постоянны и в показанном на рисунке положении противонаправлены. Для данного положения найти угловые ускорения стержней АВ и ВD, если . (8 баллов)

12. Механизм состоит из шарнирно соединенных стержней, движущихся в  плоскости своего расположения (рис. 2.12). Стержни  и  равномерно вращаются в одну сторону с угловой скоростью . Расстояния  . Для показанного положения механизма найти скорость и ускорение точки D. (8 баллов)

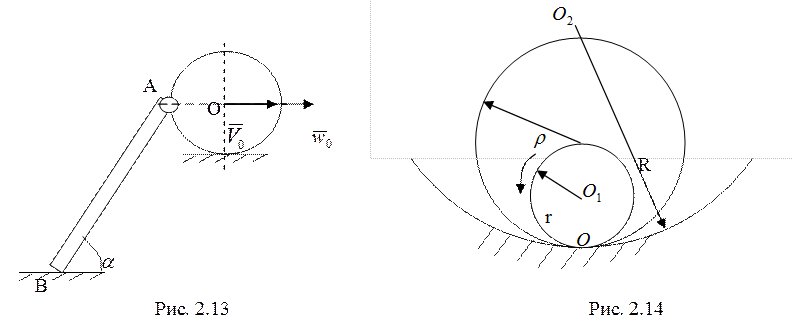
13. Стержень АВ длины  шарнирно прикреплен к ободу диска радиуса  и движется с диском в одной плоскости (рис. 2.13). Диск катится без скольжения по прямолинейным рельсам так, что его центр движется ускоренно, имея скорость  и ускорение . Найти скорость и ускорение точки В в показанном положении, если при этом угол . (8 баллов)

14. Диск радиуса  расположен внутри кольца радиуса , помещенного в неподвижную лунку радиуса  (рис. 2.14). Тела перекатываются в плоскости рисунка при отсутствии проскальзывания. Угловая скорость диска равна . Найти угловую скорость кольца. (3 балла)

15.

В плоском механизме (рис. 2.15)стержень ОА равномерно вращается в указанном направлении с угловой скоростью , а ползун D равномерно скользит в указанном направлении со скоростью . Длины стержней , . Для указанного положения механизма определить угловые скорости и угловые ускорения стержней АВ и BD. (9 баллов).

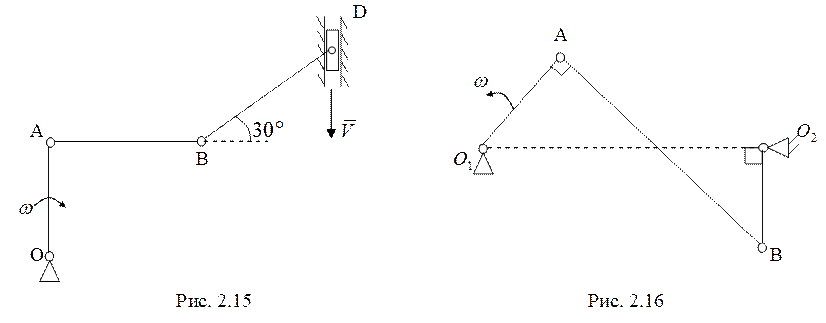
16. Стержень  вращается с угловой скоростью , приводя в движение плоский механизм (рис. 2.16). Расстояния  , . В показанном на рисунке положении найти угловую скорость стержня . (7 баллов)

17. Прямой круговой конус с углом при вершине  и радиусом основания  катится без скольжения по такому же неподвижному конусу (рис. 2.17). Найти в показанном на рисунке положении радиус кривизны траектории ближайшей «к нам» точки М конуса. (8 баллов)

18. Скорости вершин треугольной пластины (рис. 2.18) перпендикулярны ее плоскости, сонаправлены и . Угол , . Найти угловую скорость пластины и положение ее мгновенной оси вращения в показанный на рисунке момент времени. (6 баллов)