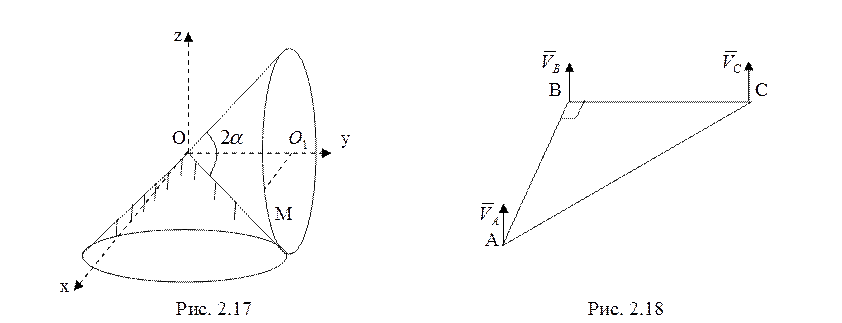 |
19. Пластинка проигрывателя (рис. 2.19) вращается с
постоянной угловой скоростью ![]() . Звуковая дорожка имеет
форму спирали Архимеда
. Звуковая дорожка имеет
форму спирали Архимеда ![]() ,
, ![]() . Найти абсолютную скорость иглы и скорость
иглы относительно пластинки в зависимости от угла
. Найти абсолютную скорость иглы и скорость
иглы относительно пластинки в зависимости от угла ![]() поворота
звукоснимателя ОА. (7 баллов)
поворота
звукоснимателя ОА. (7 баллов)
20. Стержень, изогнутый по дуге окружности радиуса ![]() (рис. 2.20), вращается замедленно
вращается вокруг оси, проходящей через точку О перпендикулярно плоскости
рисунка с угловой скоростью
(рис. 2.20), вращается замедленно
вращается вокруг оси, проходящей через точку О перпендикулярно плоскости
рисунка с угловой скоростью ![]() и угловым ускорением
и угловым ускорением ![]() . Кольцо М одновременно надето на этот
стержень и на неподвижный стержень, изогнутый по дуге окружности того же
радиуса
. Кольцо М одновременно надето на этот
стержень и на неподвижный стержень, изогнутый по дуге окружности того же
радиуса ![]() , с центром в точке О. В показанном
положении определить скорость и ускорение кольца М. (2 балла)
, с центром в точке О. В показанном
положении определить скорость и ускорение кольца М. (2 балла)
21.
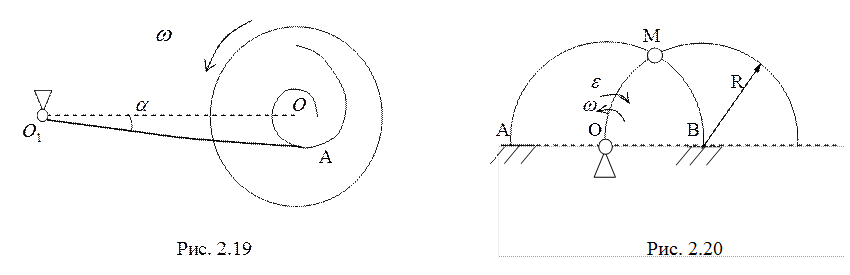 |
22. Стержень АВ длины ![]() движется
в плоскости рис. 2.22, скользя концами по неподвижным направляющим так, что
скорость точки А
движется
в плоскости рис. 2.22, скользя концами по неподвижным направляющим так, что
скорость точки А ![]() . По стержню АВ движется точка М
с относительной скоростью
. По стержню АВ движется точка М
с относительной скоростью ![]() . При какой скорости
. При какой скорости ![]() в показанном положении при
в показанном положении при ![]() абсолютное ускорение точки М в середине
стержня направлено вдоль стержня? (9 баллов)
абсолютное ускорение точки М в середине
стержня направлено вдоль стержня? (9 баллов)
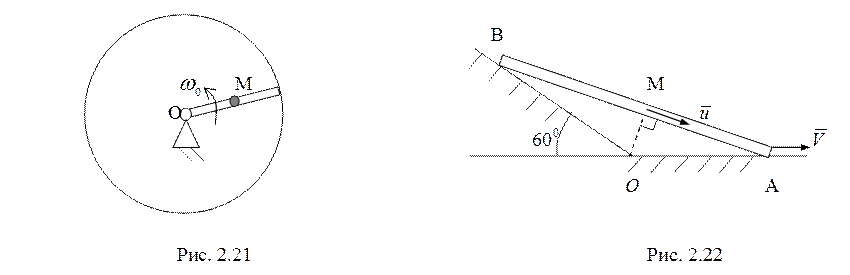
23. Тележка А скатывается с постоянной скоростью ![]() по наклонной плоскости, сматывая
нерастяжимый трос с барабана радиуса
по наклонной плоскости, сматывая
нерастяжимый трос с барабана радиуса ![]() и заставляя последний
вращаться (рис. 2.23). Найти зависимость между составляющей угловой скорости
барабана
и заставляя последний
вращаться (рис. 2.23). Найти зависимость между составляющей угловой скорости
барабана ![]() и длиной пути, пройденного тележкой из
точки
и длиной пути, пройденного тележкой из
точки ![]() . Провисанием троса пренебречь. (3 балла)
. Провисанием троса пренебречь. (3 балла)
24. 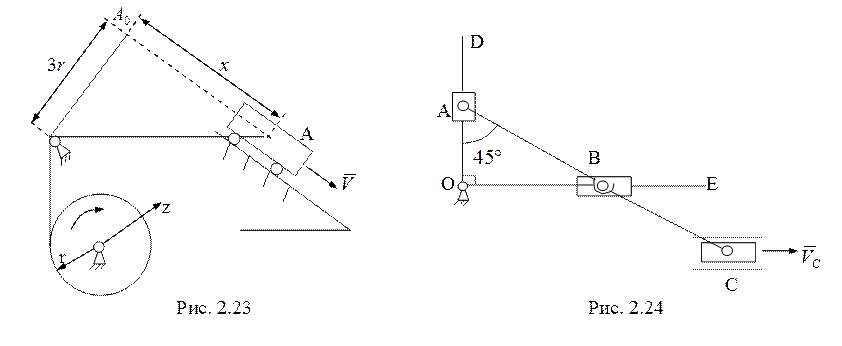
Точка С плоского механизма (рис. 2.24) движется
вправо с постоянной скоростью ![]() .
. ![]() . В указанном положении найти угловую
скорость и угловое ускорение угольника DOE. (13 баллов)
. В указанном положении найти угловую
скорость и угловое ускорение угольника DOE. (13 баллов)
25. Точка М движется в плоскости ![]() согласно
уравнениям
согласно
уравнениям ![]() . Плоскость
. Плоскость ![]() вращается
вокруг оси
вращается
вокруг оси ![]() с угловой скоростью
с угловой скоростью ![]() . Найти абсолютное ускорение точки М в тот
момент времени после начала движения, когда оно направлено вдоль прямой,
соединяющей точку М с началом координат. (7 баллов)
. Найти абсолютное ускорение точки М в тот
момент времени после начала движения, когда оно направлено вдоль прямой,
соединяющей точку М с началом координат. (7 баллов)
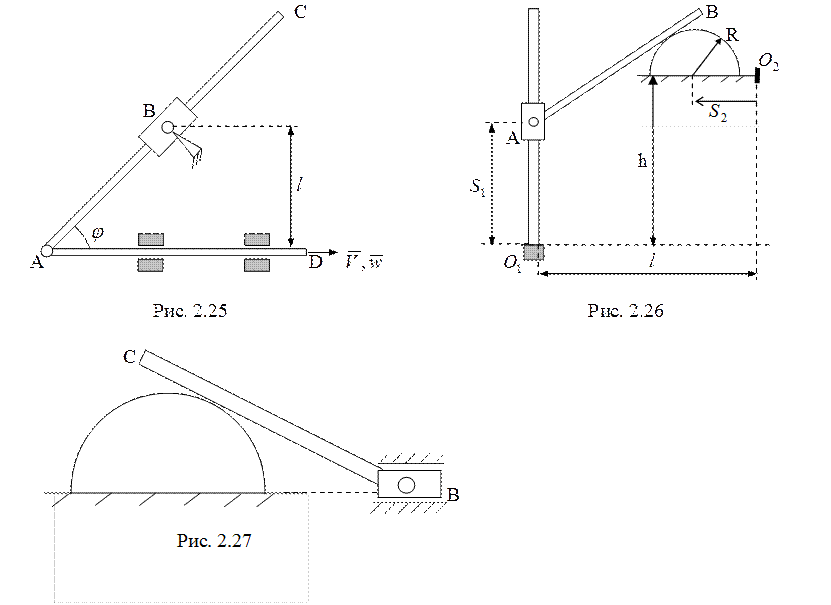
26. Стержень AD движется в направляющих
вправо, имея скорость ![]() и ускорение
и ускорение ![]() (рис. 2.25). Расстояние от точечной муфты
В до стержня AD равно
(рис. 2.25). Расстояние от точечной муфты
В до стержня AD равно ![]() . Найти угловую скорость
и угловое ускорение стержня АС в положении, определяемом углом
. Найти угловую скорость
и угловое ускорение стержня АС в положении, определяемом углом ![]() . (3 балла)
. (3 балла)
27. По неподвижной стойке скользит втулка А по закону ![]() . К втулке шарнирно прикреплен стержень АВ,
движущийся в плоскости рис. 2.26 и опирающийся на полуцилиндр радиуса
. К втулке шарнирно прикреплен стержень АВ,
движущийся в плоскости рис. 2.26 и опирающийся на полуцилиндр радиуса ![]() . Полуцилиндр движется по горизонтальной
плоскости по закону
. Полуцилиндр движется по горизонтальной
плоскости по закону 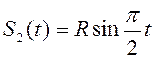 . Размеры
. Размеры ![]() .
Найти угловую скорость и угловое ускорение стержня АВ в момент времени
.
Найти угловую скорость и угловое ускорение стержня АВ в момент времени ![]() . (8 баллов)
. (8 баллов)
28.
 |
3. Решение задач
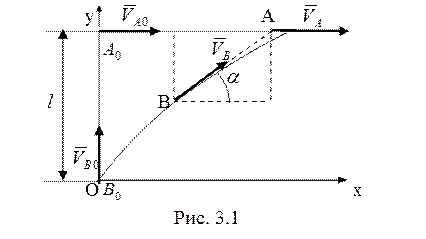 1.1-й способ. Введем в плоскости
движения систему координат
1.1-й способ. Введем в плоскости
движения систему координат ![]() (рис. 3.1). Тогда закон
движения точки А в этой системе координат имеет вид:
(рис. 3.1). Тогда закон
движения точки А в этой системе координат имеет вид:
![]() .
.
Условие того, что скорость точки В всегда направлена на текущее положение точки А выражается в виде
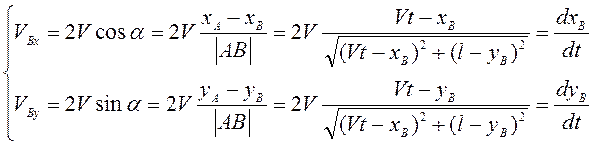
В
момент встречи расстояние ![]() .
.
Обозначим ![]() . Тогда
. Тогда
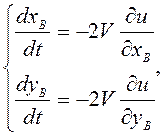 или
или 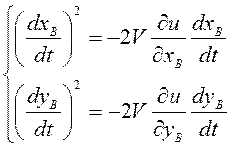
Складывая последние равенства, имеем
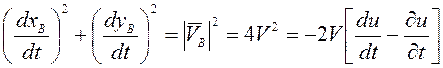 , или
, или 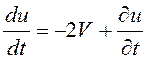 .
.
Частная
производная 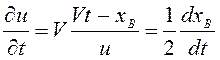 , то есть
, то есть 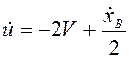 .
Интегрируя по времени последнее равенство, имеем
.
Интегрируя по времени последнее равенство, имеем 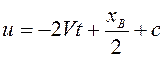 . Произвольная
постоянная интегрирования определяется из начальных условий
. Произвольная
постоянная интегрирования определяется из начальных условий
![]() ; т.е.
; т.е. ![]() , или
, или ![]() .
. 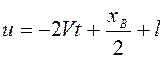
В
момент встречи ![]() , т.е.
, т.е. 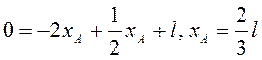 .
.
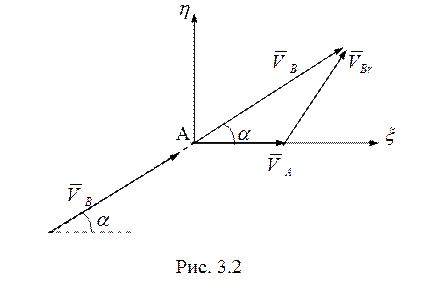 2-й способ. Введем
подвижную систему отсчета
2-й способ. Введем
подвижную систему отсчета ![]() , связанную с движущейся
точкой А (рис. 3.2). Тогда по теореме сложения скоростей для точки В
, связанную с движущейся
точкой А (рис. 3.2). Тогда по теореме сложения скоростей для точки В ![]() , или
, или ![]() . В
проекциях на подвижные оси:
. В
проекциях на подвижные оси:
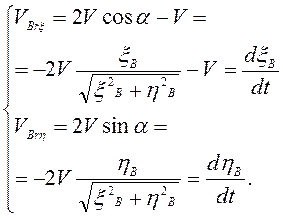
Аналогично
первому способу ![]() .
.
Тогда 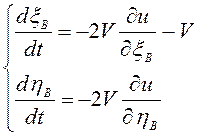 ,
или
,
или 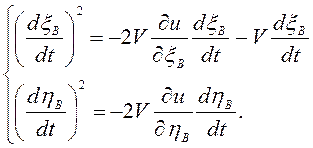
Сложением последних равенств имеем
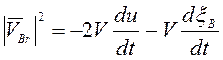 (3.1)
(3.1)
Из треугольника, построенного на векторах относительной, переносной и абсолютной скоростей точки В имеем
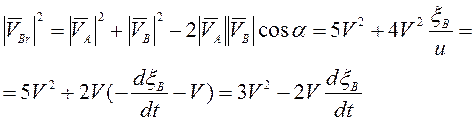 .
.
Подстановка
полученного выражения в (3.1) дает 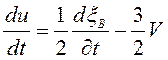 . Интегрированием
имеем
. Интегрированием
имеем 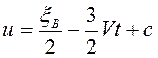 . Из начальных условий
. Из начальных условий ![]() следует, что
следует, что ![]() ,
, 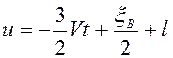 .
.
В момент встречи ![]() (путь,
пройденный точкой А). Отсюда
(путь,
пройденный точкой А). Отсюда 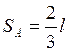 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.