Ответ: 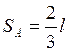 .
.
 2.1-й способ. Без ограничения общности
можем считать, что
2.1-й способ. Без ограничения общности
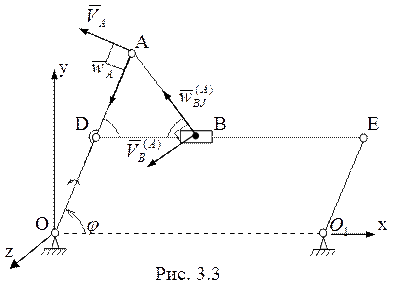
можем считать, что ![]() . Введя систему координат
. Введя систему координат ![]() (рис. 3.3) в текущий момент времени имеем
(рис. 3.3) в текущий момент времени имеем
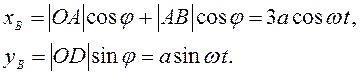
Дифференцированием по времени находим составляющие скорости и ускорения точки В
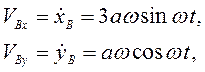
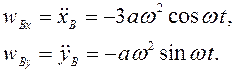
При
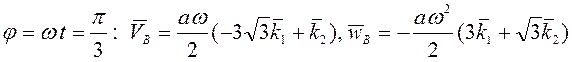 .
.
2-й способ. Так как стержни ОA и АВ образуют с горизонталью одинаковый угол, но вращаются в противоположном друг другу направлении, их угловые скорости и угловые ускорения
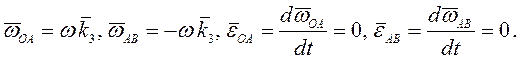
Рассматривая плоскопараллельное движение стрежня АВ имеем
![]() . (3.2)
. (3.2)
Для
стержня ОА ![]() . Скорость поворота точки В относительно
точки А
. Скорость поворота точки В относительно
точки А ![]() и направлена как показано на рис. 3.3. Проецированием
(3.2) на оси координат при
и направлена как показано на рис. 3.3. Проецированием
(3.2) на оси координат при ![]() имеем
имеем
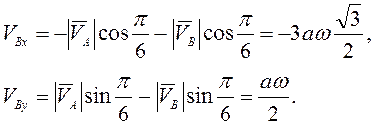
Для ускорения точки В
![]() . (3.3)
. (3.3)
Ускорение
точки А ![]() (рис. 3.3). Осе-стремительное ускорение
точки В относительно полюса А
(рис. 3.3). Осе-стремительное ускорение
точки В относительно полюса А ![]() и направлено как
показано на рис. 3.3. Проецируя (3.3) на оси координат при
и направлено как
показано на рис. 3.3. Проецируя (3.3) на оси координат при ![]() , имеем
, имеем
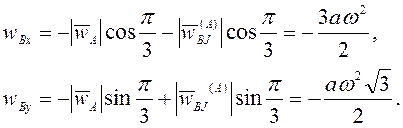
В итоге приходим к ответу.
Ответ: 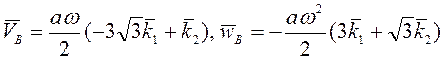 .
.
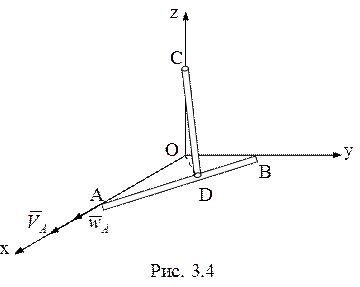 3.1-й способ. Точка С совершает
прямолинейное движение вдоль оси
3.1-й способ. Точка С совершает
прямолинейное движение вдоль оси ![]() (рис. 3.4). Ее
координата
(рис. 3.4). Ее
координата ![]() . Из треугольника
. Из треугольника ![]()
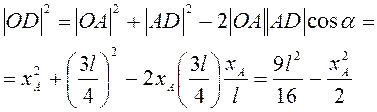 .
.
Тогда
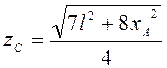 .
.
Дифференцированием координаты находим скорость и ускорение точки С.
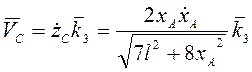
При
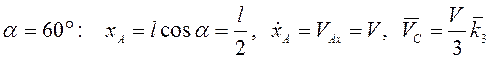 . Ускорение
. Ускорение
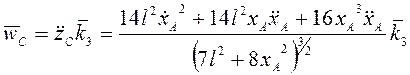 .
.
При
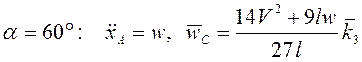 .
.
Скорости точек С и D связаны соотношением
![]() (3.4)
(3.4)
![]() .
.
Так
как 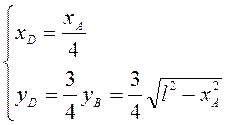 , то
, то 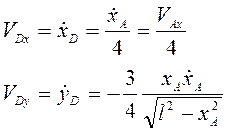 .
.
При
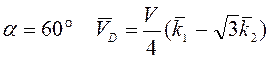 .
.
Вектор
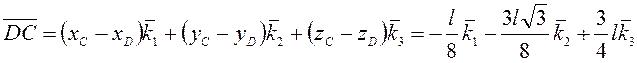 . Умножим (3.4) слева на вектор
. Умножим (3.4) слева на вектор ![]() векторно. Тогда
векторно. Тогда ![]() .
.
Так
как ![]() (при пренебрежении составляющей угловой
скорости
(при пренебрежении составляющей угловой
скорости ![]() вдоль прямой
вдоль прямой ![]()
![]() , и
, и ![]() ), то
), то 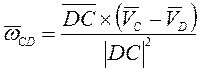 . Вычисляя векторное произведение в
последнем выражении с помощью определителя при
. Вычисляя векторное произведение в
последнем выражении с помощью определителя при ![]()
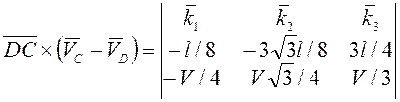
получим
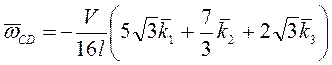 .
.
2-й способ. Рассмотрим
движение стержня АВ в плоскости ![]() (рис. 3.5). Мгновенный
центр скоростей стержня АВ
(рис. 3.5). Мгновенный
центр скоростей стержня АВ ![]() расположен как показано
на рисунке. Тогда в рассматриваемый момент времени
расположен как показано
на рисунке. Тогда в рассматриваемый момент времени ![]() . Так
как
. Так
как ![]()
![]() , т.е.
, т.е. ![]() .
.
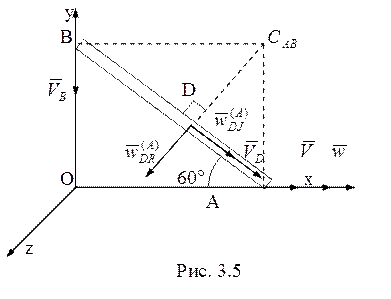 Скорость
точки D
Скорость
точки D ![]() , она перпендикулярна
, она перпендикулярна ![]() и проходит по прямой
и проходит по прямой ![]() . Угловая скорость
. Угловая скорость
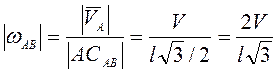 .
.
Из
условия недеформируемости стержня АВ проекции ![]() , т.е.
, т.е. ![]() . Составляющие
. Составляющие
![]()
Условие
недеформируемости стрежня CD дает соотношение ![]() , или
, или ![]() . Выписывая это соотношение через
составляющие входящих в него векторов на оси координат, имеем
. Выписывая это соотношение через
составляющие входящих в него векторов на оси координат, имеем 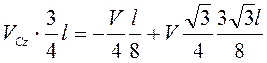 , то есть
, то есть 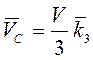 . Угловая
скорость стержня CD ищется так же, как описано в 1-м способе решения.
. Угловая
скорость стержня CD ищется так же, как описано в 1-м способе решения.
Для нахождения ускорения точки С вначале найдем
ускорение точки D. Взяв точку А за полюс, имеем ![]() .
Осестремительное ускорение
.
Осестремительное ускорение ![]() ,
, ![]() . Вращательное ускорение
. Вращательное ускорение ![]() .
.
Для определения углового ускорения ![]()
![]() рассмотрим формулу для
ускорения точки В:
рассмотрим формулу для
ускорения точки В:
![]() .
.
Проецируя ее на ось ![]() имеем
имеем ![]() ,
т.е.
,
т.е. 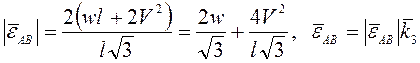 .
.
Отсюда
![]() (направление этого вектора показано на
рис. 3.5).
(направление этого вектора показано на
рис. 3.5).
Для точки С
![]() . (3.5)
. (3.5)
Вектор
![]() (так как из-за пренебрежения составляющей
угловой скорости
(так как из-за пренебрежения составляющей
угловой скорости ![]() вдоль стержня CD
вдоль стержня CD ![]() ). Для
модулей
). Для
модулей ![]() , т.е.
, т.е. ![]() , или
, или 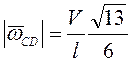 . Выписывая (3.5) в проекции на прямую
. Выписывая (3.5) в проекции на прямую ![]() избавляемся от необходимости вычисления
избавляемся от необходимости вычисления ![]() , т.к.
, т.к. ![]() . Тогда
. Тогда
![]() ,или
,или 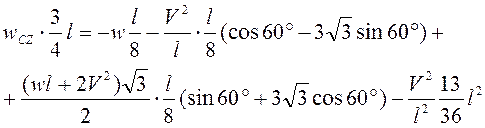 .
.
Отсюда
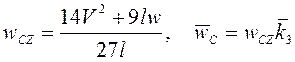 .
.
Замечание. Как видно, второй способ, использующий формулы кинематики твердого тела без формул кинематики точки, является более трудоемким.
Ответ: 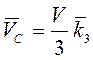 ,
, 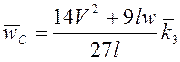 ,
, 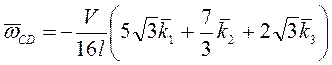 .
.
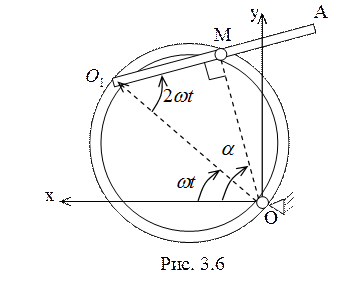 4. В рассматриваемой системе координат (рис. 3.6)
4. В рассматриваемой системе координат (рис. 3.6)
![]()
Из
треугольника ![]() расстояние
расстояние ![]() . Угол
. Угол
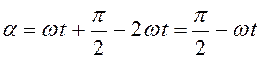
Тогда
![]() ,
,
![]() .
.
Составляющие скорости точки М
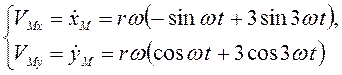
![]() ,
,
![]() Составляющие ускорения точки М
Составляющие ускорения точки М
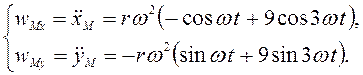
![]() ,
, ![]()
Ответ: ![]()
![]() .
.
5.1-й способ. Рассмотрим прямолинейное
движение ползуна C вдоль оси ![]() (рис. 3.7). Координата
(рис. 3.7). Координата ![]() . Не ограничивая общности можно считать,
что показанное положение соответствует начальному моменту времени
. Не ограничивая общности можно считать,
что показанное положение соответствует начальному моменту времени ![]() . Тогда угол
. Тогда угол ![]() . Из
треугольника
. Из
треугольника ![]() по теореме косинусов
по теореме косинусов ![]() По теореме синусов
По теореме синусов 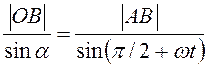 ,
то есть
,
то есть 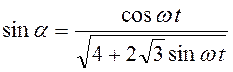 . Далее
. Далее 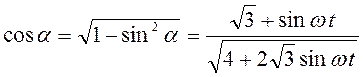
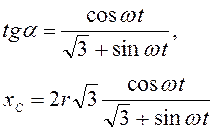
Дифференцированием
координаты ![]() по времени после упрощения полученных
выражений находим скорость и ускорение ползуна:
по времени после упрощения полученных
выражений находим скорость и ускорение ползуна:
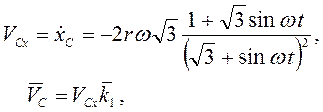
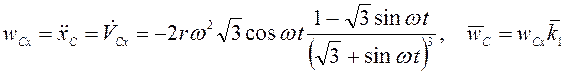 .
.
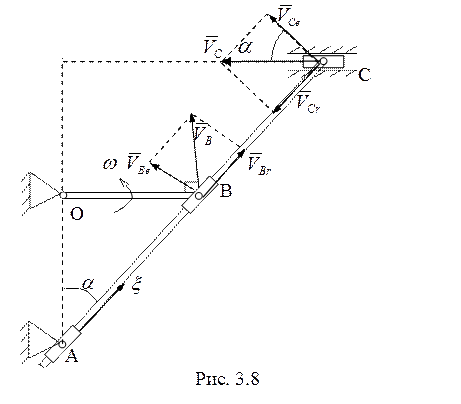 Для
заданного положения при
Для
заданного положения при ![]() :
: 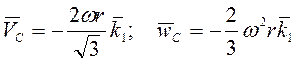 .
.
2-й способ. Свяжем подвижную систему отсчета с муфтой А, которая вращается. По теореме сложения скоростей для точки С (рис. 3.8)
![]() (3.6)
(3.6)
Для
нахождения векторов, входящих в (3.6), используем особенности движения точки В.
Для нее ![]() . Учитывая направление векторов скоростей, находим
. Учитывая направление векторов скоростей, находим
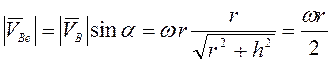 .
.
 Переносная
угловая скорость (угловая скорость муфты А)
Переносная
угловая скорость (угловая скорость муфты А) ![]() , т.е.
, т.е. ![]() . Геометрически
. Геометрически ![]() .
.
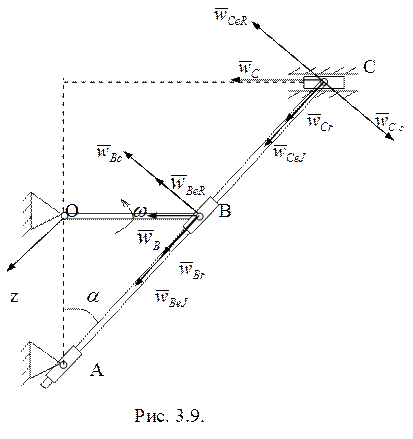
По теореме сложения ускорений (рис. 3.9)
![]() (3.7)
(3.7)
В переносном движении
![]() ,
,
![]()
Ускорение Кориолиса ![]() .
.
Для
нахождения неизвестных векторов, входящих в (3.7), также используем особенности
движения точки В. Ее ускорение (т.к. ![]() )
) ![]() .
.
С
другой стороны по теореме сложения ускорений ![]() , или
, или
![]() . (3.8)
. (3.8)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.