Выписывая
(3.8) в проекции на перпендикуляр к прямой ![]() , имеем
, имеем
![]() . Так как
. Так как ![]() , то
, то 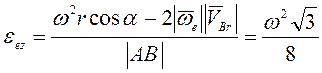 .
.
Выписывая
(3.7) в проекции на перпендикуляр к прямой ![]() имеем
имеем
![]() . Так
как
. Так
как ![]() , то
, то 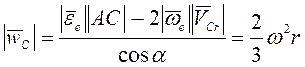 .
.
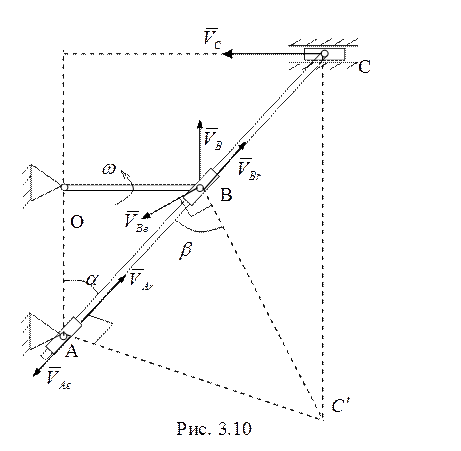
3-й способ. Рассмотрим
движение точки С как точки, принадлежащей стержню, совершающему
плоскопараллельное движение. По теореме сложения скоростей ![]()
(если
подвижная система отсчета связана со стержнем АВС) (рис. 3.10). Тогда точка ![]() является мгновенным центром скоростей рассматриваемого
стержня. Если
является мгновенным центром скоростей рассматриваемого
стержня. Если ![]() – его угловая скорость, то
– его угловая скорость, то ![]() . Угловую скорость
. Угловую скорость ![]() найдем,
используя данные о движении точки В.
найдем,
используя данные о движении точки В. ![]() , или
, или
![]() (3.9)
(3.9)
Проецируя (3.9) на перпендикуляр
к прямой ![]() имеем
имеем ![]() . Отсюда
. Отсюда
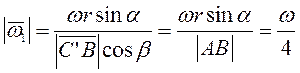 ,
,
![]() .
.
Для нахождения ускорения точки С рассмотрим теорему сложения ускорений для точки В.
![]() (3.10)
(3.10)
 Так
как
Так
как ![]() ,
, ![]() ,
, ![]() ,
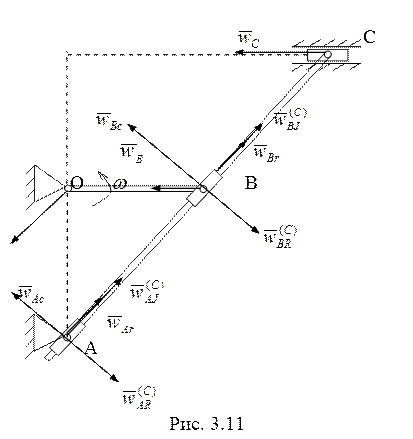
, ![]() (рис.
3.11), то выписывая (3.10) в проекции на перпендикуляр к прямой
(рис.
3.11), то выписывая (3.10) в проекции на перпендикуляр к прямой ![]() , имеем
, имеем
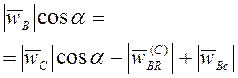 . (3.11)
. (3.11)
Для
нахождения ускорения Кориолиса ![]() вначале находим относительную
скорость
вначале находим относительную
скорость ![]() , проецируя (3.9) на прямую
, проецируя (3.9) на прямую ![]() .
.
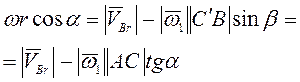 , то
есть
, то
есть ![]() ,
, 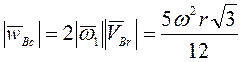 .
.
Равенство (3.11) пока не позволяет вычислить ![]() , поскольку неизвестным остается
вращательное ускорение
, поскольку неизвестным остается
вращательное ускорение ![]() . Чтобы найти его, рассмотрим теорему
сложения ускорений для точки А:
. Чтобы найти его, рассмотрим теорему
сложения ускорений для точки А:
![]() .
(3.12)
.
(3.12)
![]() ,
, ![]()
Выпишем
(3.12) в проекции на перпендикуляр к прямой ![]() :
:
![]() .
.
Ускорение Кориолиса 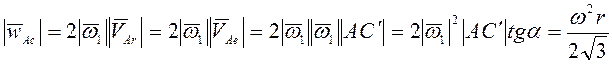 . Вращательное ускорение
. Вращательное ускорение ![]() . Поэтому
. Поэтому
![]() (3.13)
(3.13)
Совместное
решение (3.11) и (3.13) дает 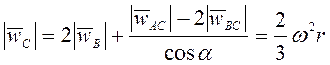 .
.
Решение показывает, что первым способом результат достигается легче, чем вторым или третьим.
Ответ: 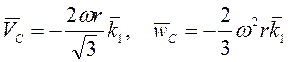 .
.
 6.1-й способ.Не
ограничивая общности будем считать, что положение системы при
6.1-й способ.Не
ограничивая общности будем считать, что положение системы при ![]() соответствует начальному моменту времени
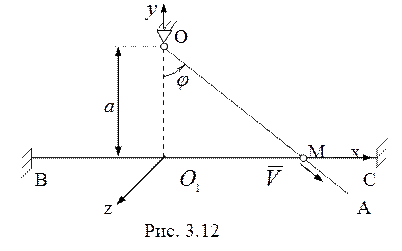
соответствует начальному моменту времени ![]() . Введенная система координат показана на
рис. 3.12. Координата точки М
. Введенная система координат показана на
рис. 3.12. Координата точки М
![]() Составляющая скорости вдоль оси
Составляющая скорости вдоль оси ![]()
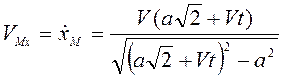 , при
, при
![]()
![]() . Составляющая
ускорения вдоль оси
. Составляющая
ускорения вдоль оси ![]()
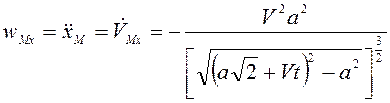 , при
, при ![]()
![]() .
.
Запишем
уравнение связи, характерное для системы: 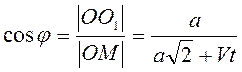 .
.
Дифференцируя его два раза по времени, получим
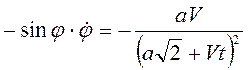 ,
, 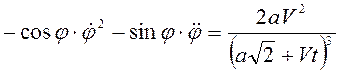 .
.
Отсюда
при ![]()
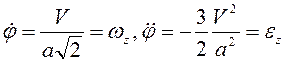 , т.е.
угловая скорость стержня ОА
, т.е.
угловая скорость стержня ОА 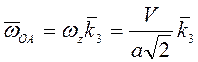 , а угловое ускорение
его
, а угловое ускорение
его 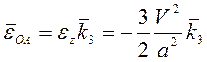 .
.
2-й способ.
Рассмотрим положение системы при ![]() (рис. 3.13). Связав
подвижную систему отсчета со стержнем ОА, по теореме сложения скоростей для
точки M имеем
(рис. 3.13). Связав
подвижную систему отсчета со стержнем ОА, по теореме сложения скоростей для
точки M имеем
![]() . Учитывая расположение входящих сюда
векторов
. Учитывая расположение входящих сюда
векторов ![]() . Так как
. Так как ![]() , то
, то 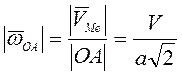 .
.
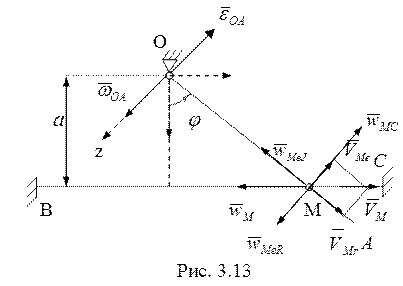 По теореме сложения ускорений для точки М
По теореме сложения ускорений для точки М
![]() (3.14)
(3.14)
Относительное
ускорение при прямолинейном равномерном движении точки М по стержню ОА ![]() .
.
Переносное ускорение
![]() . Осестремительное ускорение
. Осестремительное ускорение ![]() ,
, 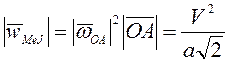 ;вращательное
ускорение
;вращательное
ускорение ![]() . Ускорение Кориолиса
. Ускорение Кориолиса 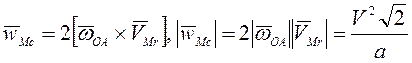 . Проецируя (3.14) на прямую
. Проецируя (3.14) на прямую ![]() имеем
имеем ![]() , т.е.
, т.е. 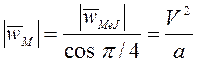 . Проецируя (3.14) на перпендикуляр к
прямой
. Проецируя (3.14) на перпендикуляр к
прямой ![]() имеем
имеем ![]() , т.е.
, т.е. 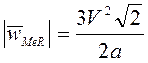 , а угловое ускорение
, а угловое ускорение 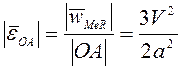 .
.
Ответ: 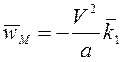 ,
, 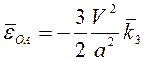 .
.
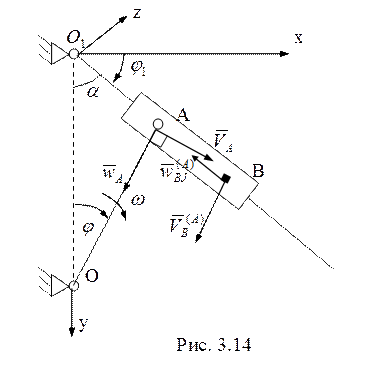 7.1-й способ. В выбранной здесь системе координат (рис. 3.14)
7.1-й способ. В выбранной здесь системе координат (рис. 3.14) ![]()
![]() . Из равнобедренного
треугольника
. Из равнобедренного
треугольника ![]() следует, что
следует, что ![]() . Тогда
. Тогда
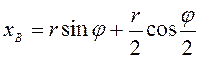 ,
, 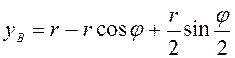 .
.
Составляющие скорости точки В
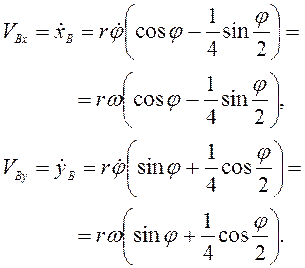
Составляющие ускорения точки В
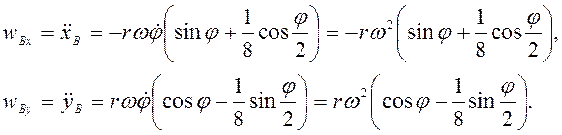
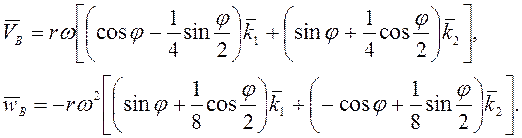
2-й способ. Рассмотрим плоскопараллельное движение кулисного камня. Скорость точки В
![]() . (3.15)
. (3.15)
При
вращательном движении ![]() ,
, ![]() .
Скорость точки В относительно полюса А
.
Скорость точки В относительно полюса А ![]() . Так
как угол поворота кулисы
. Так
как угол поворота кулисы ![]() , то
, то ![]() , и
, и ![]() .
Проецированием (3.15) на оси координат получим
.
Проецированием (3.15) на оси координат получим
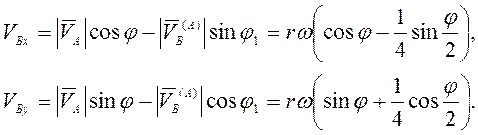
Для ускорения точки В ![]() . При
вращательном движении
. При
вращательном движении ![]() . Так как
. Так как ![]() ,
то
,
то ![]() и
и ![]() .
.
Осестремительное ускорение ![]() ,
, ![]() . Угловое ускорение
. Угловое ускорение ![]() ,
поэтому вращательное ускорение
,
поэтому вращательное ускорение ![]() , и
, и
![]() . (3.16)
. (3.16)
Проецированием (3.16) на оси координат получим
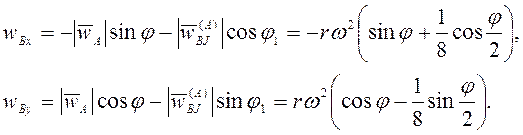
Ответ: 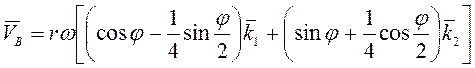 ,
,
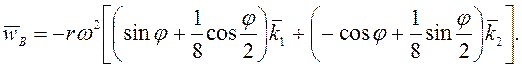
8. В рассмотренной системе координат (рис.
3.15) ![]() .
.
Дифференцированием по времени находим составляющие скорости и ускорения центра диска С:
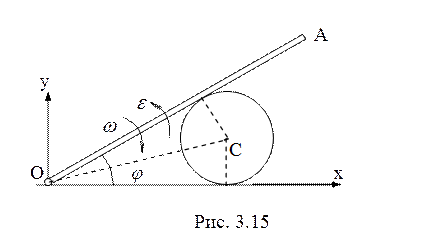
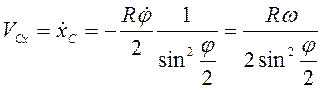 ,
,
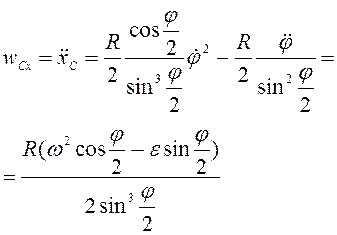 .
.
Ответ: 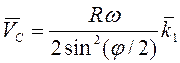 ,
, 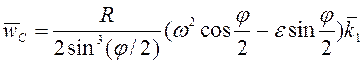 .
.
9.Точка В движется по окружности меридиана
(рис. 3.16), ее положение определяется углом ![]() .
Положение точки А на экваторе определяет угол
.
Положение точки А на экваторе определяет угол ![]() . Свяжем
эти углы с помощью уравнения связи, отражающего неизменность длины стержня:
. Свяжем
эти углы с помощью уравнения связи, отражающего неизменность длины стержня:
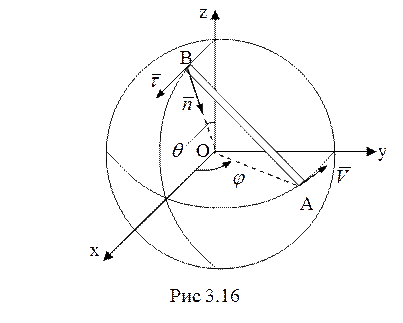
![]() (3.17)
(3.17)
Координаты точек А и В:
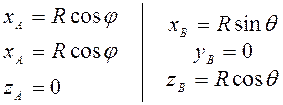
Подстановка их в (3.17) после преобразований дает
![]() , (3.18)
, (3.18)
а
при ![]() , поэтому
, поэтому ![]() .
.
Дифференцирование
(3.18) по времени дает ![]() , или
, или ![]() , при
, при ![]() :
: ![]() . Дальнейшим дифференцированием получим
. Дальнейшим дифференцированием получим 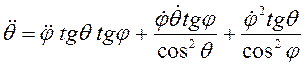 , при
, при ![]() :
: ![]() (
(![]() , так как
, так как ![]() ).
).
Скорость точки В при движении по окружности ![]() , при
, при ![]()
![]() . Ускорение точки В как сумма касательного
и нормального ускорения при движении по окружности
. Ускорение точки В как сумма касательного
и нормального ускорения при движении по окружности ![]() . При
. При ![]()
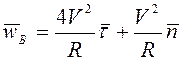 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.