Сборник задач по дисциплине "Теоретическая механика". Часть 1 (Условия 28 задач и решение задач № 1-20), страница 6

Ответ: .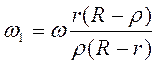

15.Рассмотрим движение точки В, принадлежащей стержням АВ и BD одновременно (рис. 3.23). Скорость этой точки

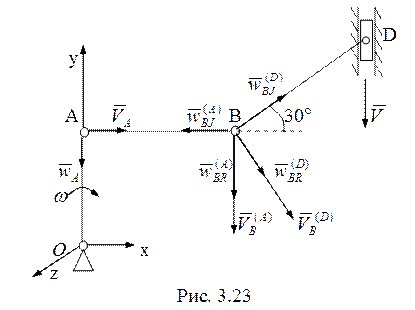
    .   (3.25)

Скорость точки А

. Скорости поворотов относительно полюсов

. (3.26)

Проецированием (3.25) на оси  и  получаем систему уравнений:

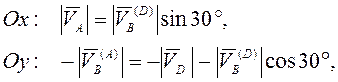
т.е. .

Учитывая (3.26)

, , , .

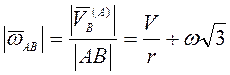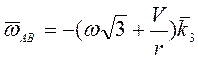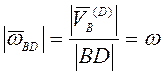Для нахождения угловых ускорений стержней АВ и BD рассмотрим ускорение точки B, взяв за полюс точки А и D:

.                                            (3.27)

Ускорение точки А как ускорение точки равномерно вращающегося стержня , . Ускорение точки D равномерно прямолинейно скользящего ползуна . Осестремительные ускорения точки В относительно полюсов

, ,

, .

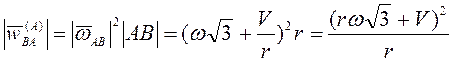Вращательные ускорения точки В относительно полюсов:

, .                                             (3.28)

Проецированием (3.27) на оси координат получим

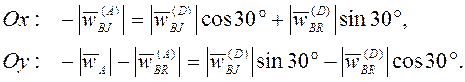
Отсюда  (т.е. вектор  направлен в сторону, противоположную показанной на рисунке 3.23, а его модуль равен вычисленной величине с противоположным знаком).

 (замечание, аналогичное сделанному для  следует иметь ввиду). Из (3.28) следует, что

, ,

, .

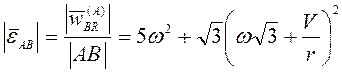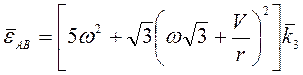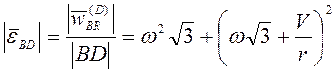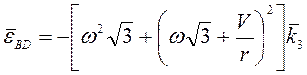Ответ: , ,

, .

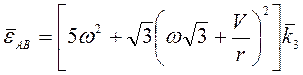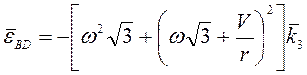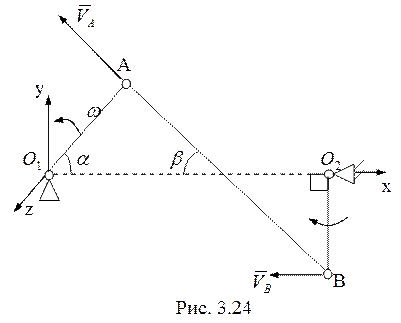16.  Уравнение связи для рассматриваемого механизма (рис. 3.24) имеет вид .  В проекциях на оси координат в данном положении оно дает равенства

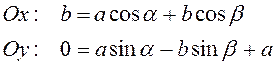   (3.29)

Возведением этих равенств в квадрат и сложением получаем, что

, т.е.

.

Скорость точки А

, ; скорость точки В .

Из условия недеформируемости стержня АВ  , т.е. .  Так как , то из (3.29) следует, что

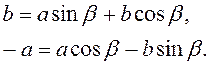
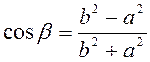Рассматривая последние равенства как линейную неоднородную систему относительно  и решая ее, получаем , т.е. .

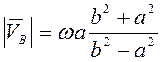Угловая скорость стержня    .

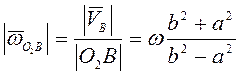Ответ: .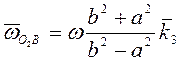

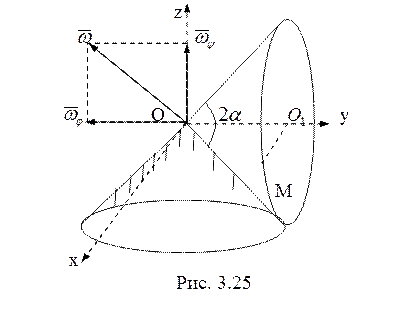17. Подвижный конус совершает вращение около неподвижной точки О (рис. 3.25). Так как траектория точки не зависит от закона вращения подвижного конуса, то для упрощения решения будем считать, что прямая  равномерно вращается вокруг оси  с угловой скоростью прецессии .

Радиус кривизны . Скорость точки М . Угловая скорость конуса  и направлена по линии касания конусов (что следует из условия качения подвижного конуса по неподвижному без проскальзывания). Тогда угловая скорость ротации . Скорость точки М

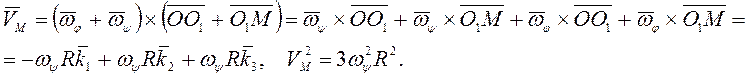
Нормальное ускорение точки М . Ускорение  . Осестремительное ускорение

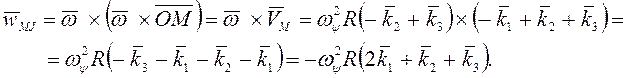
Вращательное ускорение , а угловое ускорение при регулярной прецессии конуса . Тогда , и

.

Касательное ускорение точки М 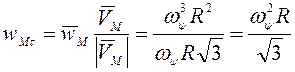, нормальное ускорение ее . Окончательно радиус кривизны .

Ответ: .

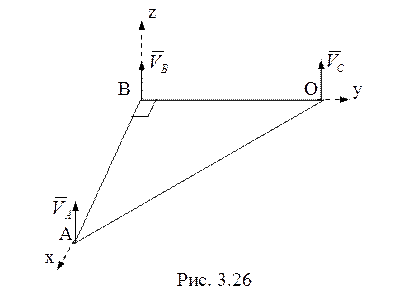18.Введенная система координат показана на рис. 3.26. Так как

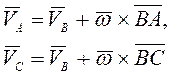        (3.30)

а векторное произведение перпендикулярно своим сомножителям, то угловая скорость  перпендикулярна оси , т.е. .

Выписывая (3.30) в проекции на ось  получим

 т.е.  и .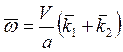

Мгновенная ось вращения пластины параллельна угловой скорости и скорость точек этой оси равна нулю. Пусть она проходит через точку D. Тогда

,                                                               (3.31)

.  Так как

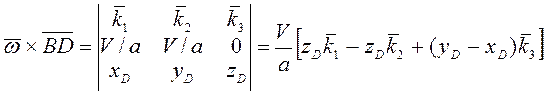, то формула (3.31) в проекциях на оси координат дает 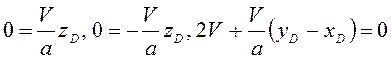. Отсюда .  Мгновенной осью вращения является прямая, лежащая в плоскости , уравнение которой .

Ответ: 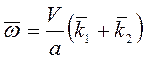, уравнение мгновенной оси вращения в плоскости :  .

19. Связав подвижную систему отсчета с вращающейся пластинкой

(рис. 3.27), запишем теорему сложения скоростей для иглы А:

          .                 (3.32)

Абсолютная скорость , переносная скорость , относительную скорость представим, используя полярную систему координат, связанную с пластинкой

.

Проецируя (3.32) на оси введенной полярной системы координат получим

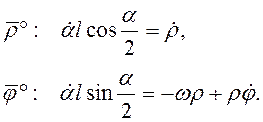                                                       (3.33)

Уравнение спирали дает 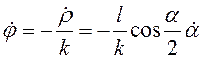. Из треугольника  . Подстановка последних выражений в (3.33) дает равенство 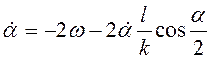, т.е. 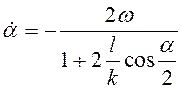. Скорость точки А 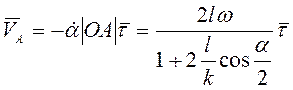, где  - единичный вектор касательной к траектории точки А.

Так как 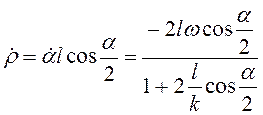, , 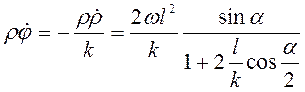то .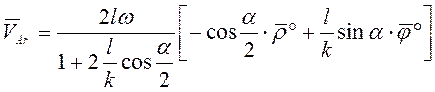

Ответ: , .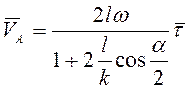

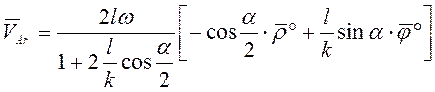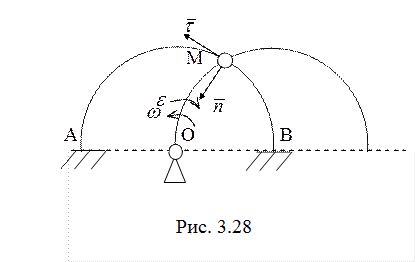20. Так как точка О, вокруг которой в плоскости рисунка вращается стержень (рис. 3.28), совпадает с центром неподвижной окружности, на которую надето кольцо М, то абсолютное и переносное движение точки М совпадают, а относительное движение кольца М по вращающемуся стержню отсутствует. Тогда скорость

,а ускорение .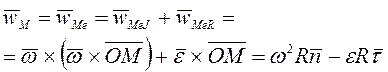

Ответ: , .