Ответ: ![]() ,
, 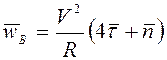 .
.
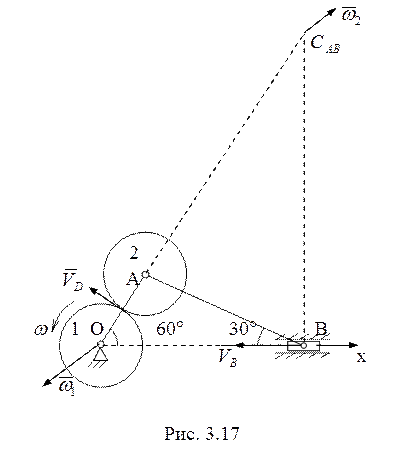 10. Скорость точки D зацепления
колес (рис. 3.17)
10. Скорость точки D зацепления
колес (рис. 3.17) ![]() . Учитывая направления векторов
скорости точек D и В мгновенным центром скоростей шатуна АВ и колеса 2
является точка
. Учитывая направления векторов
скорости точек D и В мгновенным центром скоростей шатуна АВ и колеса 2
является точка ![]() . Угловая скорость
. Угловая скорость
![]() . Расстояние
. Расстояние
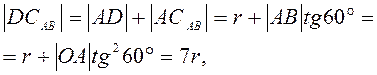
т.е.
![]() . Скорость точки В
. Скорость точки В
![]() .
.
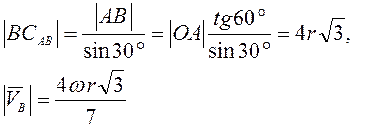
Ускорение точки В ищем, взяв за полюс точку А.
![]() (3.18)
(3.18)
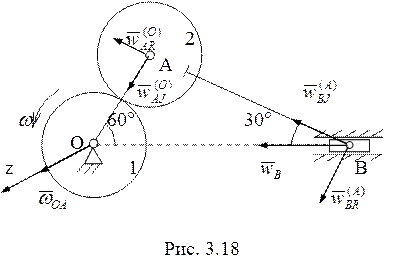 Ускорение
точки А как точки, принадлежащей вращающемуся стержню
Ускорение
точки А как точки, принадлежащей вращающемуся стержню ![]() .
Осестремительное ускорение
.
Осестремительное ускорение ![]() (рис. 3.18). Угловая
скорость
(рис. 3.18). Угловая
скорость
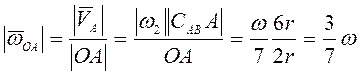 , и
, и 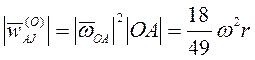 .
.
Вращательное ускорение
![]() .
.
Скорость
точки D можно представить как ![]() . Слагаемые,
входящие в последнее равенство, сонаправлены, т.е.
. Слагаемые,
входящие в последнее равенство, сонаправлены, т.е. ![]() .
.
Дифференцированием
последнего равенства по времени, имеем ![]() , или
, или ![]() (для угловых ускорений). Соответственно
(для угловых ускорений). Соответственно 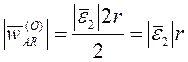 .
.
Осестремительное ускорение ![]() ,
,
![]() . Вращательное ускорение
. Вращательное ускорение ![]() ,
, ![]() .
Проецируя (3.18) на прямую
.
Проецируя (3.18) на прямую ![]() и на перпендикуляр к
ней получим соответственно
и на перпендикуляр к
ней получим соответственно
![]()
Решая
последнюю систему уравнений относительно ![]() находим
находим
![]() , т.е. ускорение точки В направленно по
горизонтали вправо.
, т.е. ускорение точки В направленно по
горизонтали вправо.
Ответ: 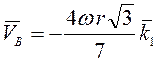 ,
, 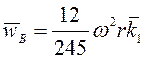 .
.
11. Рассмотрим движение точки В, принадлежащей стержням АВ и BD одновременно (рис. 3.19). Тогда скорость этой точки
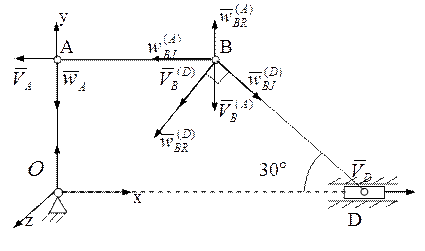
![]() (3.19), где
скорости поворота относительно полюса соответственно
(3.19), где
скорости поворота относительно полюса соответственно
![]() . Проецируя (3.19) на оси
. Проецируя (3.19) на оси ![]() и
и ![]() получим
систему уравнений для нахождения модулей скоростей поворота точки В
относительно полюсов A и D:
получим
систему уравнений для нахождения модулей скоростей поворота точки В
относительно полюсов A и D:
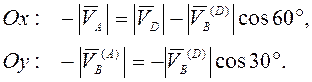
Тогда
![]() , а угловые скорости стержней
, а угловые скорости стержней
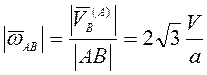 ,
, 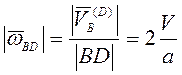 ,
, 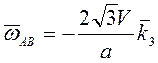 ,
, 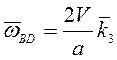 .
.
Для нахождения угловых ускорений стержней АВ и BD рассмотрим ускорение точки В, взяв также за полюс точки А и D.
![]() (3.20)
(3.20)
Ускорение
точки А как нормальное ускорение точки, равномерно движущейся по окружности
радиуса ![]() , равно
, равно 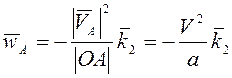 .
Ускорение точки D при прямолинейном движении
.
Ускорение точки D при прямолинейном движении ![]() .
Осестремительные ускорения точки В относительно полюсов
.
Осестремительные ускорения точки В относительно полюсов ![]() ,
,
![]() ,
, ![]() .
.
Вращательные ускорения точки В относительно полюсов
![]() ,
, ![]() (3.21)
(3.21)
Проецированием (3.20) на оси координат получим
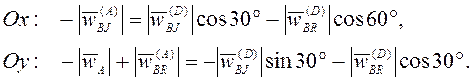
Разрешая
последнюю систему относительно модулей вращательных ускорений, получим ![]() (т.е. вектор
(т.е. вектор ![]() направлен
в сторону, противоположную направлению этого вектора, показанного на рис. 3.19).
направлен
в сторону, противоположную направлению этого вектора, показанного на рис. 3.19).
Учитывая (3.21), находим угловые ускорения стержней
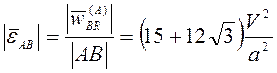 ,
, 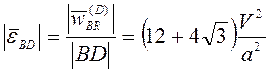 ;
;
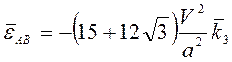 ,
, 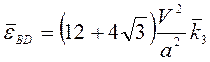 .
.
Ответ: 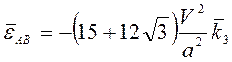 ,
, 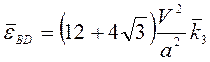 .
.
12. Рассмотрим движение точки D, принадлежащей стержням AD и BD одновременно (рис. 3.20). Скорость этой точки
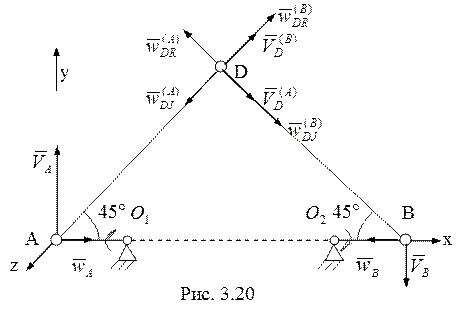
![]() .(3.22)
.(3.22)
Скорости точек А и В
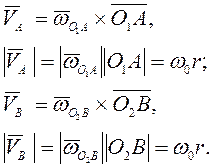
Скорости поворота точки В относительно полюсов
![]()
Проецируя
(3.22) на перпендикулярные прямые ![]() и
и ![]() получим
получим
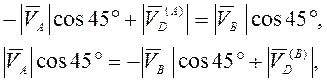
т.е.
![]() . Отсюда угловые скорости стержней AD и BD
. Отсюда угловые скорости стержней AD и BD ![]() . Из
(3.22) следует, что
. Из
(3.22) следует, что
![]() , и
, и ![]() (направлена
вправо вдоль оси
(направлена
вправо вдоль оси ![]() .
.
Для нахождения ускорения точки D также возьмем за полюс точки А и В.
![]() (3.23)
(3.23)
Ускорения
точек А и В как нормальные ускорения точек, равномерно движущихся по окружности
радиусов ![]() и
и ![]() равны
равны
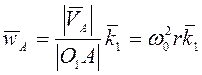 ,
, 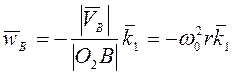 .
.
Осестремительные ускорения точки D относительно полюсов
![]()
![]()
![]()
![]() .
.
Вращательные ускорения точки D относительно полюсов
![]() ,
, ![]() .
.
Проецированием
(3.23) на прямую ![]() получим
получим
![]() , т.е.
, т.е. ![]() . Учитывая
(3.23) в проекциях на оси
. Учитывая
(3.23) в проекциях на оси
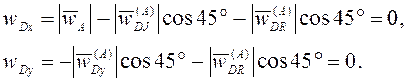
Ответ: ![]() ,
, ![]() .
.
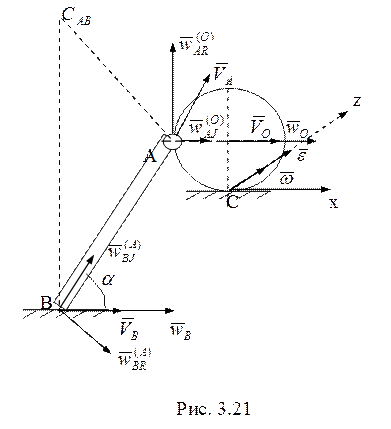 13.Из условия качения диска без
проскальзывания следует, что его мгновенный центр скоростей находится в точке С
(рис. 3.21), а скорость точки А перпендикулярна АС. Условие недеформируемости
диска дает для проекций скоростей
13.Из условия качения диска без
проскальзывания следует, что его мгновенный центр скоростей находится в точке С
(рис. 3.21), а скорость точки А перпендикулярна АС. Условие недеформируемости
диска дает для проекций скоростей ![]() , т.е.
, т.е. ![]() ,
, ![]() . Из
условия недеформируемости стержня АВ
. Из
условия недеформируемости стержня АВ ![]() , т.е.
, т.е. ![]() ,
, ![]() .
.
Для нахождения ускорения точки В примем точку А стержня АВ за полюс.
![]() (3.24)
(3.24)
Ускорение точки А находим как ускорение точки диска, взяв за полюс точку О.
![]() . Осестремительное ускорение
. Осестремительное ускорение ![]() . Угловая скорость диска
. Угловая скорость диска 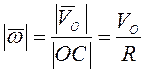 (направлена "от нас"
перпендикулярно плоскости рисунка). Тогда
(направлена "от нас"
перпендикулярно плоскости рисунка). Тогда 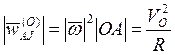 .
.
Вращательное
ускорение ![]() . Если ось
. Если ось ![]() направлена
"от нас", то
направлена
"от нас", то 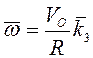 , а угловое ускорение
диска
, а угловое ускорение
диска 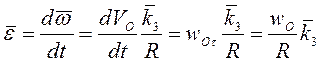 и сонаправлено с угловой скоростью диска.
Тогда
и сонаправлено с угловой скоростью диска.
Тогда ![]() .
.
Осестремительное ускорение ![]() . Мгновенный
центр скоростей стержня АВ
. Мгновенный
центр скоростей стержня АВ ![]() расположен в точке
пересечения перпендикуляров к векторам скорости точек
расположен в точке
пересечения перпендикуляров к векторам скорости точек ![]() и
и
![]() . Тогда угловая скорость стержня
. Тогда угловая скорость стержня ![]() , а
, а ![]() .
.
Вращательное ускорение ![]() . Проецированием
(3.24) на прямую
. Проецированием
(3.24) на прямую ![]() получаем
получаем
![]() , т.е.
, т.е.
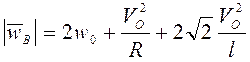 .
.
Ответ: ![]() ,
, 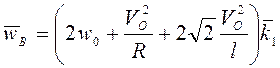 .
.
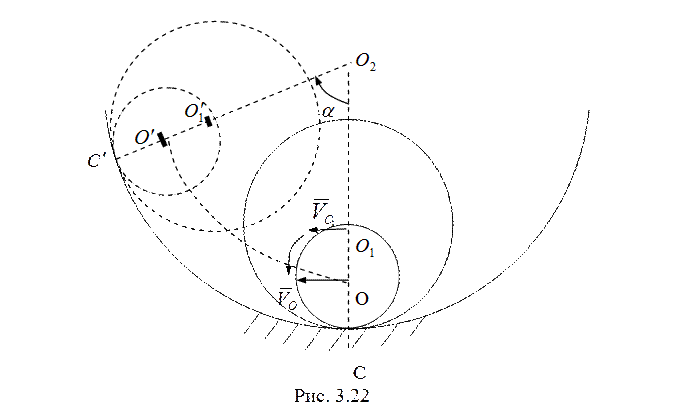 |
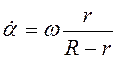 .
Аналогично, скорость
.
Аналогично, скорость 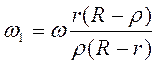 .
Вектор угловой скорости кольца сонаправлен с вектором угловой скорости диска и
направлен "на нас" перпендикулярно плоскости рисунка.
.
Вектор угловой скорости кольца сонаправлен с вектором угловой скорости диска и
направлен "на нас" перпендикулярно плоскости рисунка.Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.