Вынужденные колебания системы вещественных точек

Вынужденные колебания системы вещественных точек  в случае, когда возбуждающая сила является гармонической функцией «t»

«n» для 8=1, q=q(t)  Система с одной степенью свободы

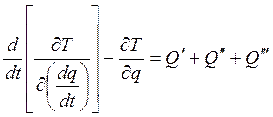
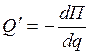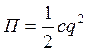 ;      - обобщающая сила соответствующая консервативным силам

 ;              обобщающая сила соответствующая силам      сопротивления (неконсервативные силы)

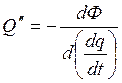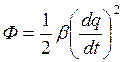
 обобщающая сила, соответствующая возмущающей силе

P-наибольшее значение  возмущающей силы

Р- циклическая частота

Т_в.с=- период возмущающей силы

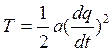 -кинетическая энергия системы

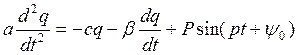- из уравнения Лагранжа второго рода

Разделим на «а», перегруппируем

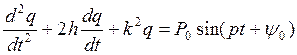    (*)  (1)

(*) Дифференциальное уравнение – неоднородное, линейное дифференциальное уравнение с постоянными коэффициентами.

q=q^*+q_одн     (2)

q= общее решение однородного уравнения и частное решение неоднородного уравнения

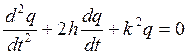
1) Случай малого сопротивления (h<k)

2) h=k          

3) Случай большого сопротивления  h>k:

Частное решение неоднородного дифференциального уравнения (1) ищем в форме правой части

 частота совпадает с частотой возмущающей силы

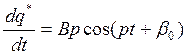 подставим в уравнение (1)

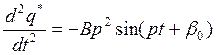 подставим в уравнение (1)

(3)

Т.к последнее равенство есть тождество, то коэффициенты стоящие перед одноименной тригонометрической функций одного и того же аргумента, должны быть равны.

Сравним при 

Сравним при

Неизвестные Р₀, , уравнений тоже два:

уравнение возведем в квадрат и сложим

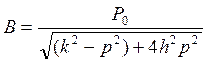
Нижнее равенство поделим на верхнее почленно, получим:

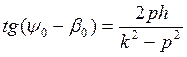
(4)

1)h<k

   (**)

В этом случае обобщенная координата будет совершать сложное движение, состоящее из наложенных одно на другое одновременных движений: затухающих собственных колебаний и набухающих вынужденных колебаний

q^* -вынужденные колебания системы вещественных точек

Для определения констант интегрирования зададим начальные условия (два)

При t=0; q=q₀

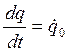
Определим константу интегрирования:

 (***)

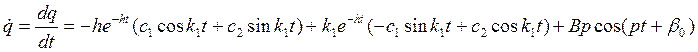В (**) и в (***) подставим t=0

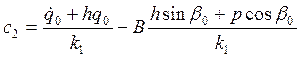
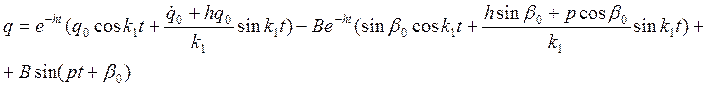
Предположим: q₀=0,  тогда второе и третье слагаемое обобщаются и система будет совершать сложные движения, а последние слагаемое отражает условие вынуждающей силы.

В некоторый момент времени t^* собственными колебаниями системы можно будет пренебречь по сравнению с вынуждающей силой. Момент t^* называется временем установления, а установившийся процесс называется установившиеся колебания:

2)h=k

3)h>k

Анализ вынужденных колебаний системы.

;      

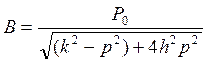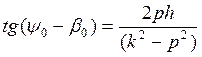
Вынужденные колебания системы вещественных точек не зависит от нормальных условий, а полностью определяется возмущающей силой, инерциальными и упругими свойствами системы и сопротивлением среды.

Введем:

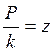 - отношение  частоты вынуждающей силы к частоте собственных(свободных) колебаний системы

;  

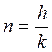
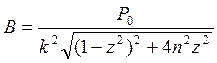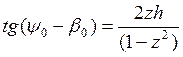
Сдвиг фаз.

1) z=0, то возмущающая сила постоянна

     

2) z=1,  то частота собственных колебаний совпадет с частотой вынуждающей силы- резонанс

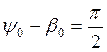            не зависит от сопротивления среды

3)                (независимо от сопротивления среды)

В общем случае.

Кривая сдвига фаз:

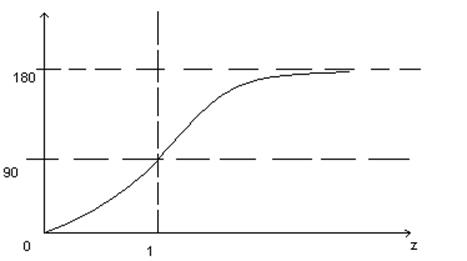
Анализ амплитуды колебаний.

Обозначим: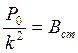

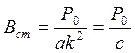-квазицирующий  коэффициент

Удлинение, которое получает пружина жесткости «с» под действием постоянной нагрузки Р₀

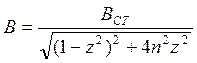- амплитуда вынужденных колебаний будет зависеть от отношения частот  при одном  и том же фиксированном n или h

Обозначим - коэффициент динамичности

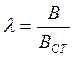
т.к. амплитуда вынужденных колебаний больше чем её отклонение при статическом действии нагрузки Р₀, то

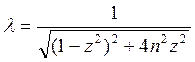
1)  z=0; =1 (возмущающая сила постоянна)

2)  z=1; 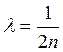 (резонанс)

3)  ;   (p>k)

Зависимость коэффициента динамичности «» от частного отношения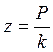

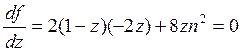       (Ищем экстремум функции)

z₁=0; 

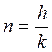 (пусть сопротивление среды мало)

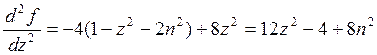
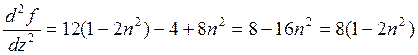
z=z₂

a) ; т.е 

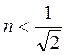
если 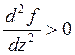, то функция f(z) –возрастает  а коэффициент динамичности убывает

z=z₂     

б) ; т.е   

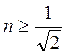
если 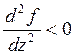  f(z)- убывает , коэффициент динамичности возрастает

z=z₂