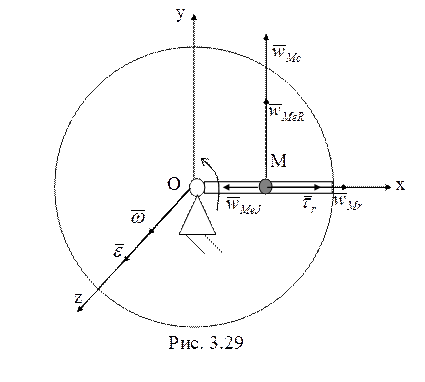
 21. Рассмотрим текущее положение точки М (рис. 3.29).
Ее ускорение согласно теореме сложения ускорений
21. Рассмотрим текущее положение точки М (рис. 3.29).
Ее ускорение согласно теореме сложения ускорений ![]() .
Ускорение при прямолинейном движении относительно диска
.
Ускорение при прямолинейном движении относительно диска ![]() .
Переносное ускорение за счет вращения диска
.
Переносное ускорение за счет вращения диска ![]() , где
осестремительное ускорение
, где
осестремительное ускорение
![]() ,
,![]() , а вращательное
ускорение
, а вращательное
ускорение
![]() . Ускорение Кориолиса
. Ускорение Кориолиса
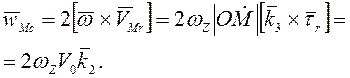 Условием того, что ускорение точки М
всегда направлено по радиусу, является
Условием того, что ускорение точки М
всегда направлено по радиусу, является
![]() .
.
Оно дает дифференциальное уравнение первого порядка
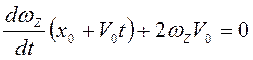 , решаемое
совместно с начальным условием
, решаемое
совместно с начальным условием ![]() .
.
Разделением
переменных получим 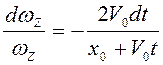 , и последующим интегрированием
, и последующим интегрированием 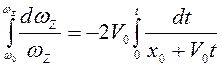 , далее
, далее
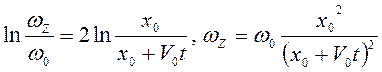 . Так как
. Так как ![]() , то
угол поворота
, то
угол поворота
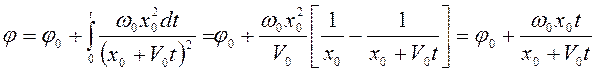 .
.
Не
ограничивая общности угол поворота можно отсчитывать от начального положения
радиуса ОМ, при этом ![]() .
.
Ответ: 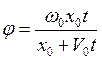 .
.
22. Движение точки М (рис. 3.30) представляет собой
сложение движений, и ее ускорение вычисляем по теореме сложения ускорений ![]() . Относительное ускорение при прямолинейном
движении точки по стержню
. Относительное ускорение при прямолинейном
движении точки по стержню ![]() . Переносное движение
представляет собой движение
. Переносное движение
представляет собой движение 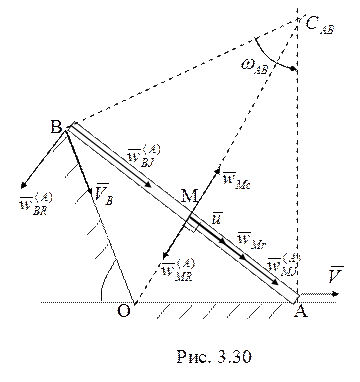 точки
плоскопараллельно движущегося стрежня АВ, в которой в этот момент времени
оказалась точка М, т.е. середины стержня. Переносное ускорение
точки
плоскопараллельно движущегося стрежня АВ, в которой в этот момент времени
оказалась точка М, т.е. середины стержня. Переносное ускорение
![]() .
.
Ускорение
![]() , осестремительное ускорение
, осестремительное ускорение ![]() , вращательное ускорение
, вращательное ускорение ![]() . Ускорение Кориолиса
. Ускорение Кориолиса ![]() .
.
Условие
направленности ускорения точки М в показанном положение вдоль стержня
получается проецированием теоремы сложения ускорений на перпендикуляр к прямой ![]() , т.е.
, т.е.
![]() . (3.34)
. (3.34)
Мгновенный
центр скоростей стержня АВ (точка ![]() ) лежит на пересечении
перпендикуляров к векторам скоростей точек А и В. Для угловой скорости
) лежит на пересечении
перпендикуляров к векторам скоростей точек А и В. Для угловой скорости
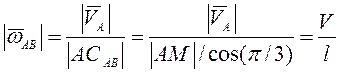 .
.
Для
нахождения углового ускорения стержня ![]() рассмотрим
движение точки В. Ее ускорение
рассмотрим
движение точки В. Ее ускорение
![]() . (3.35)
. (3.35)
Осестремительное
ускорение ![]() ,
, ![]() .
Вращательное ускорение
.
Вращательное ускорение ![]() . Проецированием (3.35)
на перпендикуляр к прямой
. Проецированием (3.35)
на перпендикуляр к прямой ![]() получим
получим
![]() , т.е.
, т.е. 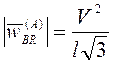 .
.
Отсюда
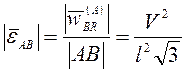 . Подставив найденные значения в (3.34) получим
. Подставив найденные значения в (3.34) получим
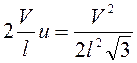 , или
, или 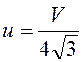 .
.
Ответ: 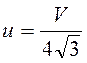 .
.
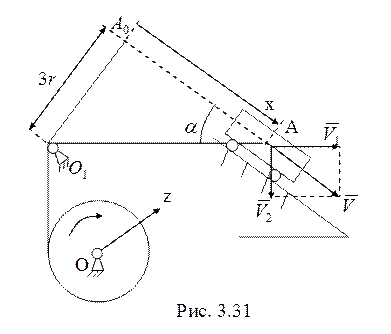 23. Скорость тележки
23. Скорость тележки ![]() (рис. 3.31)складывается из
скорости
(рис. 3.31)складывается из
скорости ![]() за счет удлинения участка троса
за счет удлинения участка троса ![]() и скорости
и скорости ![]() за счет
поворота этого участка вокруг точки
за счет
поворота этого участка вокруг точки ![]() . Тогда
. Тогда 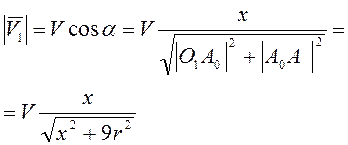 .
.
С
другой стороны ![]() , поэтому
, поэтому 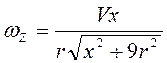 .
.
Ответ:
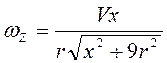 .
.
24. Запишем теорему сложения скоростей для точки В, связав подвижную систему отсчета с угольником DOE (рис. 3.32)
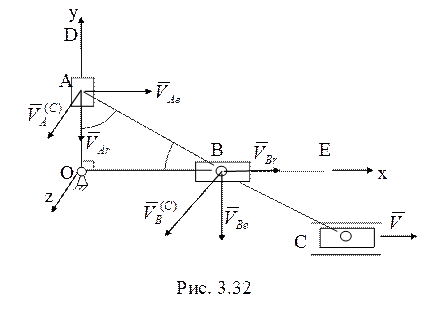
![]() . (3.36)
. (3.36)
Взяв
точку С за полюс имеем ![]() .
.
С
другой стороны ![]() .
.
В
проекциях на оси ![]() и
и ![]() (3.36)
дает систему двух уравнений:
(3.36)
дает систему двух уравнений:
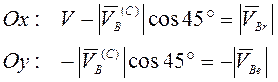 (3.37)
(3.37)
Она
содержит три неизвестные величины ![]() ,
, ![]() ,
, ![]() . Чтобы
число уравнений равнялось числу неизвестных используем теорему сложения
скоростей в проекциях на оси
. Чтобы
число уравнений равнялось числу неизвестных используем теорему сложения
скоростей в проекциях на оси ![]() ,
, ![]() для точки А:
для точки А: ![]() . Так
как
. Так
как ![]() ,
, ![]() ,
, ![]() , то в проекции на ось
, то в проекции на ось ![]() :
:
![]() . (3.38)
. (3.38)
Совместным решением (3.37) и (3.38) получим
![]() ,
, ![]() ,
, ![]() .
.
Отсюда
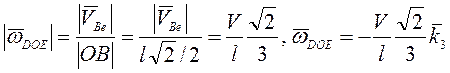 .
.
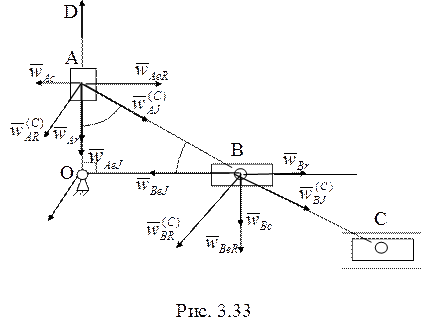
Для нахождения углового ускорения угольника DOE используем теорему сложения ускорений для точек В и А (рис. 3.33).
![]() (3.39)
(3.39)
Ускорение
точки В ![]() . Ускорение
. Ускорение ![]() . Осестремительное
ускорение
. Осестремительное
ускорение ![]() ,
, 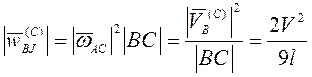 .
.
Вращательное ускорение ![]() .
.
Переносное ускорение
точки В ![]() , его осестремительная составляющая
, его осестремительная составляющая ![]() ,
, 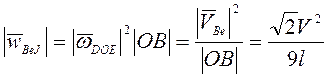 , а
вращательная составляющая
, а
вращательная составляющая ![]() . Ускорение Кориолиса
. Ускорение Кориолиса 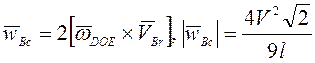 .
.
В проекциях на оси координат (3.39) даст
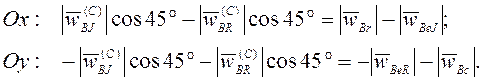 (3.40)
(3.40)
Последние
два уравнения содержат три неизвестных ![]() ,
, ![]() ,
, ![]() .
.
Для нахождения уравнений, позволяющих найти все неизвестные, воспользуемся теоремой сложения ускорений для точки А:
![]() . (3.41)
. (3.41)
![]() , где
осестремительное ускорение
, где
осестремительное ускорение ![]() , вращательное
ускорение
, вращательное
ускорение ![]() .
.
Переносное
ускорение ![]() , его осестремительная составляющая
, его осестремительная составляющая ![]() , вращательная составляющая
, вращательная составляющая ![]() ,
, ![]() .Ускорение
Кориолиса
.Ускорение
Кориолиса ![]() . Тогда (3.41) в проекции на ось
. Тогда (3.41) в проекции на ось ![]() даст
даст
![]() (3.42).
(3.42).
Совместным
решением (3.40) и (3.42) получим ![]() , и потому
, и потому ![]() .
.
Ответ:
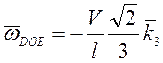 ,
, ![]() .
.
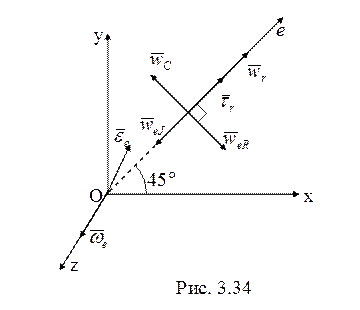 25. Согласно уравнениям относительного
движения точки
25. Согласно уравнениям относительного
движения точки ![]() , т.е. точка М движется
относительно плоскости
, т.е. точка М движется
относительно плоскости ![]() прямолинейно вдоль оси
прямолинейно вдоль оси ![]() так что
так что 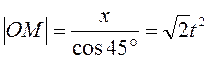 (рис.
3.34). По теореме сложения ускорений
(рис.
3.34). По теореме сложения ускорений ![]() . Относительное ускорение
при прямолинейном движении
. Относительное ускорение
при прямолинейном движении 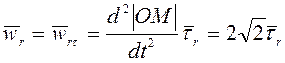 (
(![]() - единичный вектор касательной к траектории
в относительном движении).
- единичный вектор касательной к траектории
в относительном движении).
Переносное
ускорение за счет вращения точки вместе с плоскостью ![]()
![]() , его осестремительная составляющая
, его осестремительная составляющая ![]() ,
, ![]() ;
вращательная составляющая
;
вращательная составляющая ![]() . Угловое ускорение
. Угловое ускорение 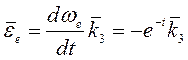 , и
, и ![]() .
.
Ускорение
Кориолиса 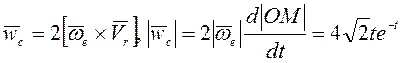 .
.
Тогда
условием того, что абсолютное ускорение направлено вдоль прямой ![]() , является
, является ![]() , т.е.
это имеет место при
, т.е.
это имеет место при ![]() . Вектор абсолютного ускорения
точки в этот момент времени направлен вдоль оси
. Вектор абсолютного ускорения
точки в этот момент времени направлен вдоль оси ![]() и равен
и равен
![]() .
.
Ответ:
![]() .
.
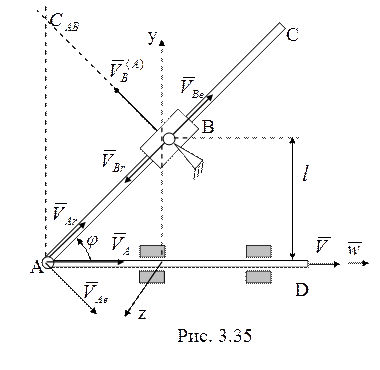 26.1-й
способ. Во введенной системе координат (рис. 3.35)
26.1-й
способ. Во введенной системе координат (рис. 3.35) ![]() .
Дифференцированием по времени получим
.
Дифференцированием по времени получим 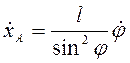 , или
, или 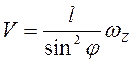 . Отсюда
. Отсюда 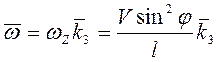 .
.
Дальнейшим
дифференцированием получим 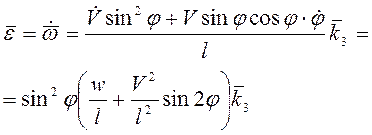 .
.
2-й
способ. Рассмотрим покой точки В как результат сложения движения стержня АВ
и проскальзывания ползуна вдоль стержня. Тогда по теореме сложения скоростей ![]() , то есть
, то есть ![]() . Так
как
. Так
как ![]() , то проецируя теорему сложения скоростей
на перпендикуляр к прямой
, то проецируя теорему сложения скоростей
на перпендикуляр к прямой ![]() получим
получим ![]() . Так как
. Так как 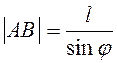 , то
, то 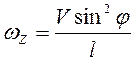 . Дифференцированием аналогично 1-му
способу находим угловое ускорение стержня АВ.
. Дифференцированием аналогично 1-му
способу находим угловое ускорение стержня АВ.
3-й
способ. Построим мгновенный центр
скоростей стержня АВ как точку пересечения перпендикуляров к векторам ![]() и
и ![]() . Тогда
. Тогда 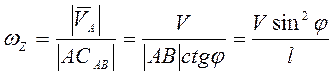 . Дифференцированием находим угловое ускорение.
. Дифференцированием находим угловое ускорение.
4-й
способ. Свяжем неподвижную систему координат с вращающейся муфтой В. По
теореме сложения скоростей для точки А ![]() . Тогда
. Тогда
![]() , или
, или 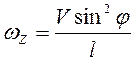 . Дифференцированием
находим угловое ускорение.
. Дифференцированием
находим угловое ускорение.
Ответ:
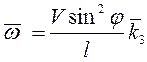 ,
, 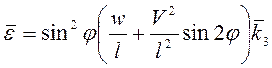 .
.
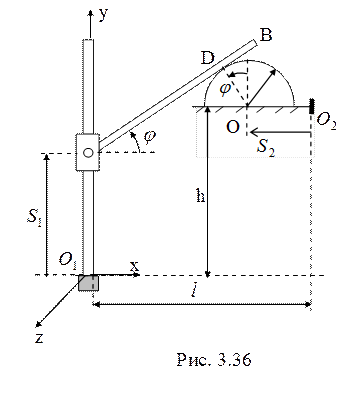 27.Запишем
уравнения связи для рассматриваемой системы с двумя степенями свободы (рис. 3.36):
27.Запишем
уравнения связи для рассматриваемой системы с двумя степенями свободы (рис. 3.36):
![]() . В проекциях на оси координат
. В проекциях на оси координат
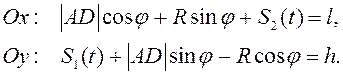
Умножением
первого равенства на ![]() , второго на
, второго на ![]() и вычитанием из него первого получим
и вычитанием из него первого получим
![]() . (3.43)
. (3.43)
При
![]() , и из (3.43) следует
, и из (3.43) следует ![]() , или
, или 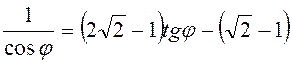 . Так
как
. Так
как 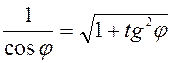 , то возведением левой и правой части в
квадрат получим
, то возведением левой и правой части в
квадрат получим ![]() , откуда
, откуда
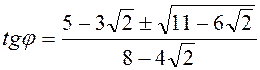 . Но
. Но ![]() . Выбирая
корень, соответствующий
. Выбирая
корень, соответствующий ![]() , имеем при
, имеем при ![]() .
.
Дифференцированием (3.43) по времени получим
![]() , (3.44)
, (3.44)
т.е.
при 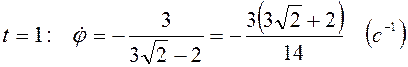 ,
, 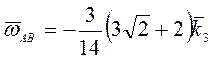 .
.
Дифференцированием (3.44) по времени получим
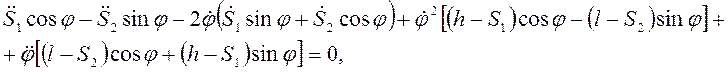
т.е.
при 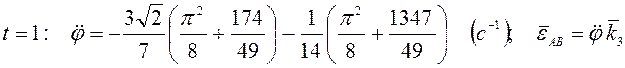 .
.
Ответ:
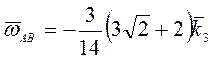 ,
, 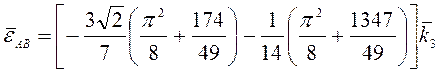 .
.
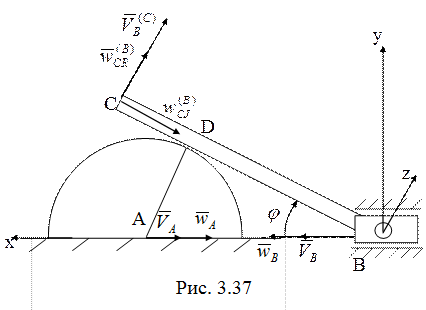 28.Согласно
уравнению связи для рассматриваемой системы (рис. 3.37)
28.Согласно
уравнению связи для рассматриваемой системы (рис. 3.37) 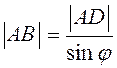 ,
т.е.
,
т.е. 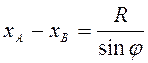 . Дифференцированием по времени получим
. Дифференцированием по времени получим 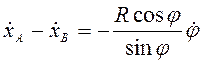 , или
, или 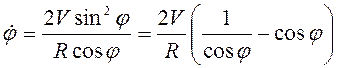 .
.
Угловая
скорость ![]() . При
. При ![]() . Дальнейшим
дифференцированием получим
. Дальнейшим
дифференцированием получим
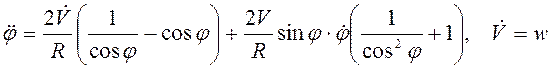 . Угловое ускорение
. Угловое ускорение ![]() .
При
.
При 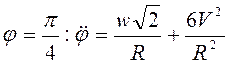 .
.
Для точки С:
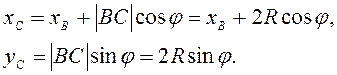
Составляющие скорости точки С
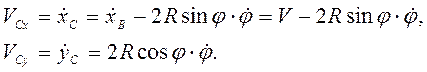
При
![]() .
.
Составляющие ускорения точки С
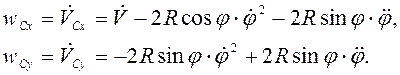
При
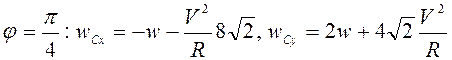 ,
, ![]() .
.
Замечание. Скорость и ускорение точки С также можно вычислить по формулам, характерным для плоскопараллельного движения стержня ВС.
![]()
![]() .
.
Составляющие скорости точки С вдоль осей координат
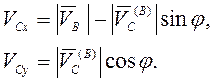
Ускорение
точки С ![]() . Осестремительное ускорение
. Осестремительное ускорение ![]() ,
, ![]() . Вращательное
ускорение
. Вращательное
ускорение ![]() ,
, ![]() .
.
Составляющие ускорения точки С вдоль осей координат
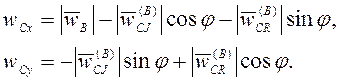
Подставляя значения,
соответствующие углу ![]() , приходим к ранее полученному
результату.
, приходим к ранее полученному
результату.
Ответ:
![]() ,
, 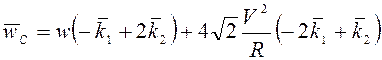
Библиографический список
1. Курс теоретической механики / Под редакцией К.С. Колесникова. М.: Изд–во МГТУ им. Н.Э. Баумана, 2000.
2. Мещерский И.В. Задачи по теоретической механике. С-Пб: Лань, 1998.
3. Пятницкий Е.С., Трухан Н.М., Ханукаев Ю.И., Яковенко Г.Н. Сборник задач по теоретической механике. М.: Наука, 1980.
4. Исмагамбетов М.У., Рощанский В.И. Задачи по основам механики. С-Пб, Изд. центр СПбГМТУ, 1999.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.