Корректирующая способность кода, верность передачи сообщений кодом, страница 7

§Классификация корректирующих кодов.

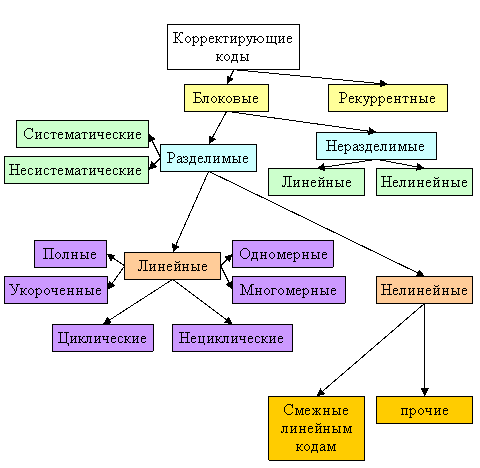
Разделимым кодом разрядности n называется код, в каждой комбинации которого можно выделить позиции, на которых стоят информационные и проверочные символы.

Распространение получили только коды, у которых во всех комбинациях эти позиции постоянны.

Разделимые коды обозначаются как (n, k)- код, где n – разрядность, а k – число информационных символов.

Блоковые разделимые коды образуются при первом способе построения комбинаций корректирующего кода.

Разделимый код содержит N = 2^k комбинаций.

Неразделимым называется код, в комбинациях которого невозможно выделить позиции, на которых стоят информационные и проверочные символы. Неразделимые коды образуются при помощи второго способа построения комбинаций.

Пример: код с постоянным весом, равным 2, является неразделимым кодом.

Разделимый блоковый код называется систематическим, если в каждой его комбинации первые k позиций заняты информационными символами, а последние r позиций – проверочными.

Если через a_i (i=1,..k) обозначить значения информационных символов , а через b­_j (j=1,..r) значения проверочных, то каждая комбинация систематического кода имеет следующую структуру: V = (a₁ a_2….. a_k b­₁ b­_2…. b­_r)

Если комбинации кода имеют другую структуру, то код называется несистематическим.

Например, несистематическим является код Хемминга со структурой комбинаций V = (b­₁ b­₂ a₁ b­₃ a₂ a₃ a₄). Проверочные символы занимают позиции равные степеням двойки.

§Принцип исправления ошибок в комбинациях линейных кодов.

Заметим, что количество комбинаций синдрома 2^r всегда меньше, чем число векторов ошибок 2ⁿ, т.к. r<n. С другой стороны, как видно из формулы (11) вид комбинации синдрома определяется вектором ошибок. Это означает, что соответствие между вектором ошибок и комбинациями синдрома однозначно, но не взаимнооднозначно, т.е. несколько векторов ошибок порождают одну и ту же комбинацию синдрома. Эта ситуация характеризуется следующим графом: