Корректирующая способность кода, верность передачи сообщений кодом, страница 2

Действительно искажения символов комбинаций кода при передаче по такому каналу считаются независимыми событиями. Вероятность искажения нуля равна вероятности искажения единицы, т.е. p₀ = p₁ = p, где p – вероятность искажения двоичного символа.

При таких условиях передача любого символа по каналу характеризуется всего двумя числами: вероятностью искажения символа – p и вероятностью правильной передачи символа        q =  1 – p.  .

Двоичный симметричный канал обычно представляют следующим графом:

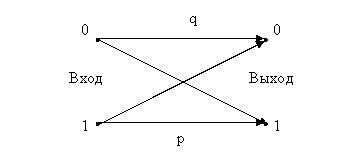
Граф, задающий двоичный симметричный канал без памяти

Для ДСК при вероятности искажения символа p<q справедливо утверждение: если на выход канала пришла запрещенная комбинация, то вероятность того, что она появилась в результате ошибок меньшей кратности, больше, чем вероятность того, что она появилась в результате ошибок большей кратности.

Отсюда следует, что для минимизации вероятности появления ложной кодовой комбинации на выходе декодера при передаче информации по ДСК кодом с исправлением ошибок необходимо, чтобы в первую очередь обеспечивалось исправление ошибок меньшей кратности. Такой принцип исправления ошибок определяет следующее правило разбиения множества запрещенных комбинаций U на подмножества А_i: запрещенная комбинация u_j приписывается такой кодовой V_i, от которой она отличается в наименьшем числе символов. Исправление ошибок в соответствии с указанным принципом получило название исправление по принципу максимального правдоподобия.

Определим теперь каким минимальным d должен обладать код, который по методу максимального правдоподобия позволял бы исправлять ошибки кратности от 1 до ν_и. В соответствии с этим методом запрещенная комбинация, получаемая из некоторой кодовой в результате искажения ν_и символов должна отличаться от любой кодовой больше, чем ν_и символами, то есть расстояние между любыми двумя кодовыми комбинациями d > 2ν_и или учитывая, что d – целое,

     (2)

Пример: 

ν_и=2

d≥5