Корректирующая способность кода, верность передачи сообщений кодом, страница 3

V₃ → V₁

V₄ → V₁

V₅ → V₂

V₆ → V₂

 

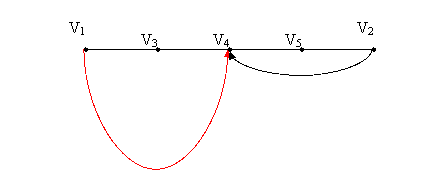
V₄ находится на одинаковом расстоянии от V₁ и V₂, следовательно, .

Найдем теперь каким d должен обладать код, который бы позволил обнаруживать ошибки кратности ν₀ и менее, а ошибки кратности ν_и и менее исправлять.

Прежде всего заметим, что для того чтобы код мог исправлять ошибки  какой-либо кратности, он их должен прежде обнаружить, следовательно, максимальная кратность исправляемых ошибок должна удовлетворять неравенству:

ν_{0 ≥} ν_и

При получении комбинации с ν₀ ошибками это должна быть запрещенная комбинация, которая не исправляется в те комбинации, которые код исправляет. Отсюда d кода должно удовлетворять условию:

           (3)

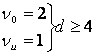
Проверим это на графе:

Обнаруживаются ν₀, исправляются ν_и.

То как используется d конкретного кода, определяет разработчик системы связи.

Формула (3) является наиболее общей. Формулы (1) и (2) получаются из нее как частные случаи. Если код используется только для обнаружения ошибок, то ν_и = 0, следовательно .

Если ν_{0 =} ν_и, то есть максимальная кратность исправляемых ошибок равна максимальной кратности обнаруживаемых ошибок, то при подстановке в (3) ν_{0 =} ν_и получаем формулу (2).

Ранее мы рассматривали задачу нахождения минимальной разрядности кода n_min, если известно число передаваемых сообщений N и подлежащие исправлению вектора ошибок.

Поставим обратную задачу: определить, какое максимальное число N_max комбинаций существует в коде разрядности n, которые бы в совокупности образовывали корректирующий код с кодовым расстоянием d.