Методы исследования типовых звеньев ТАУ и систем в целом на базе аналоговых вычислительных машин с помощью типовых воздействий, переходных процессов и частотных характеристик САУ, страница 9

6 Как оперировать значениями частот АФЧХ апериодического звена первого порядка?

7 Какие значения частот соответствуют на ЛАЧХ интегрирующего звена частоте сопряжения и пересечения линии lg (ω)?

8 Как, пользуясь АФЧХ типового звена, определить АЧХ, ФЧХ, ВЧХ и МЧХ ?

IV Лабораторная работа 4

Исследование устойчивости системы автоматического управления с помощью алгебраических и частотных критериев

 Целью лабораторной работы является изучение и практическое применение критериев устойчивости САУ и влияния обратной  связи на формирование граничных условий устойчивости.

Общие указания

     Рассмотрите систему, состоящую из регулятора (апериодического звена первого порядка) и объекта (колебательного звена или апериодического второго порядка), структурная схема которой приведена на  рисунке 4.1.  

 

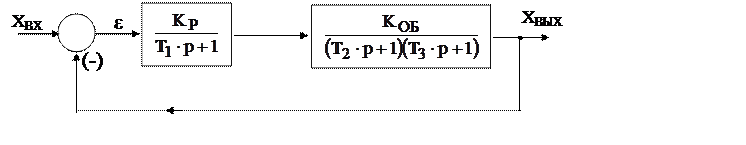                               Рисунок   4.1 ─  Структурная схема САУ

          Для получения ожидаемого характера переходного процесса при известных динамических характеристиках объекта и регулятора, а так же определения параметров регулятора для достижения желаемого процесса при известных параметрах объекта руководствуйтесь следующим.

Запишите характеристическое уравнение системы :

        (1 + р∙Т₁)(1 + р∙Т₂)(1 + р∙Т₃) + к = 0.                              (4.1)    

          Это уравнение соответствует системе регулирования, содержащей три инерционных звена с постоянными времени Т₁ ,Т₂ , Т₃  и общим коэффициентом усиления К= К_р∙ К_об. Необходимо, например, по критерию Гурвица найти  предельное  значение Кпр, при котором система перестает быть устойчивой. Уравнение (4.1) следует представить в виде :

  Т₁ ∙Т₂ ∙Т₃∙ р³  +(Т₁∙Т₂  + Т₂∙ Т₃  + Т₁ ∙Т₃ )р² + (Т₁ +Т₂ +Т₃)∙ р +1+к = 0.        (4.2)

    Согласно критерию устойчивости Гурвица система устойчива, если вы- полняются неравенства :

,

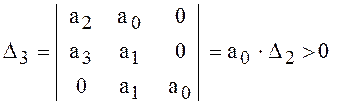при положительности всех коэффициентов, входящих в уравнение (4.2) :

а₀  > 0,  а₁  > 0, а₂  > 0,  а₃  > 0;  a₂ ∙ a1 ─ a₃ ∙ a₀  > 0;                   (4.3)

где а₀ = 1+к ;     а₁ = Т₁ +Т₂ +Т₃;   а₂ = Т₁∙Т₂  + Т₂∙ Т₃  + Т₁ ∙Т₃ ;   а₃ = Т₁ ∙Т₂ ∙Т₃.

Неравенство (4.3) может быть переписано в виде :

(Т₁∙Т₂  + Т₂∙ Т₃  + Т₁ ∙Т₃ )(Т₁ +Т₂ +Т₃)  > (1+К)·Т₁ ∙Т₂ ∙Т₃.            (4.4)

Разделив левую часть на сомножитель Т₁ ∙Т₂ ∙Т₃, предварительно раскрыв скобки числителя и введя обозначения :

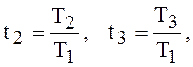
можно получить :

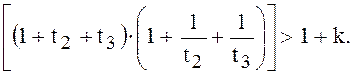                       (4.5)

Из последнего неравенства следует, что оно становится неверным при :

К≥ К_ПРЕД  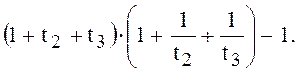=                                  (4.6)                          

          Выражение (4.6) показывает, что предельный коэффициент усиления К_пред замкнутой системы определяется не абсолютной величиной постоянных времени звеньев, а их относительным (4.2) значением : К_пред тем больше, чем больше t₂ и  t₃, т.е. чем существеннее отличаются постоянные времени друг от друга. В частном случае, когда Т₁ =Т₂ =Т₃= Т, то К_пред = 8, исходя из уравнения (4.4). Аналогично определив предельный коэффициент усиления из частотного критерия Михайлова или D-разбиения, можно сравнить полученные значения и убедиться, что они отличаются лишь погрешностью метода вычисления.

Порядок выполнения работы на АВМ

1 Соберите на наборном поле аналоговой машины схему набора замкнутой системы автоматического регулирования (рисунок 4.2).

2 Установите согласно варианта задания параметры звеньев электронной модели САУ из таблицы 4.1.

По заданному преподавателем критерию устойчивости и результатам экспериментального переходного процесса, зафиксированном на экране осциллографа, определите предельный коэффициент усиления САУ.

 

Рисунок  4.2 ─ Схема набора замкнутой САУ

Таблица 4.1 – Параметры замкнутой САУ

параметры CАУ	№ варианта
	1	2	3	4	5	6	7	8
UВХ, В	5	10	15	20	25	30	35	40
КР	0.2	0.4	0.6	0.7	0.5	0.9	0.6	0.8
КОБ	0.3	0.4	1.0	0.6	0.7	0.4	0.2	0.9
Т1, с	0.02	0.45	0.05	0.60	0.025	0.04	0.10	0.35
Т2, с	0.25	0.055	0.040	0.650	0.035	0.40	0.075	0.060
Т3, с	0.5	0.15	0.90	0.35	0.55	0.80	0.450	0.070

Содержание отчета

Отчет по лабораторной работе должен содержать :

     - теоретическое изложение использованного критерия устойчивости;

     - схему набора и параметры модели исследуемой системы;

     - график переходного процесса системы и значения показателей качества переходных процессов (времени регулирования и перерегулирования);

     - таблицу значений экспериментальных данных, анализ устойчивости САУ и значение предельного коэффициента усиления, вычисленного по одному из заданных преподавателем критериев устойчивости. 

Контрольные вопросы

1 В чем  состоит соответствие  электронной модели и структурной схемы САУ ?

2 За счет каких элементов схемы модели возможно моделирование  САУ третьего порядка ?

3 Как коэффициент главной обратной связи влияет на граничный коэффициент усиления САУ ?

4 Сформулируйте определение критериев устойчивости Гурвица, Рауса, Михайлова, Найквиста, D-разбиения ?

В чем состоят способы  увеличения или уменьшения  граничного коэффициента усиления САУ ?

ПЕРЕЧЕНЬ  ССЫЛОК

1 Куропаткин П.В. Теория автоматического управления. Учебное пособие. – М.: Высш. школа, 1973.- 253 с.

2 Ирклиевский В.Д. Автоматическое управление . Учебное пособие. – К.: Лыбидь, 1992.- 192 с.

3 Попов Е.П. Автоматическое регулирование и управление. – М.: Высш. школа, 1966.- 388 с.

4 Фурунжиев Р.И. Вычислительные машины и программирование.- Минск, Высш. школа, 1981.- 240 с.