Методы исследования типовых звеньев ТАУ и систем в целом на базе аналоговых вычислительных машин с помощью типовых воздействий, переходных процессов и частотных характеристик САУ, страница 6

Переходная характеристика вида рис. 2.1, описываемая экспонентой (2.1), является решением следующего дифференциального уравнения :

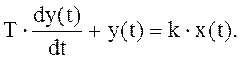                                               (2.3)

Следовательно, динамика апериодического звена описывается обыкновенным дифференциальным уравнением первого порядка с постоянными коэффициентами. Дифференциальному уравнению звена (2.3) соответствует характеристическое уравнение :

Тр + 1= 0,                                                      (2.4)

корнем которого является значение

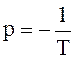.                                                            (2.5)

Вместо дифференциального уравнения динамики звена (2.3) часто записывают так называемую передаточную функцию его :

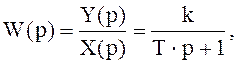                                             (2.6)

т.е. отношение изображения по Лапласу выходной величины к  изображению по Лапласу входной величины при нулевых начальных условиях. Чтобы перейти от передаточной функции к дифференциальному уравнению, нужно переписать выражение  (2.6) следующим образом :

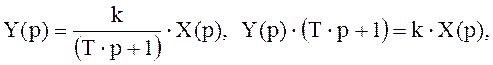                          (2.7)

после чего надо раскрыть скобки и произвести замену  р→ dy/dt.

2.1.2 Апериодическое звено второго порядка и его параметры

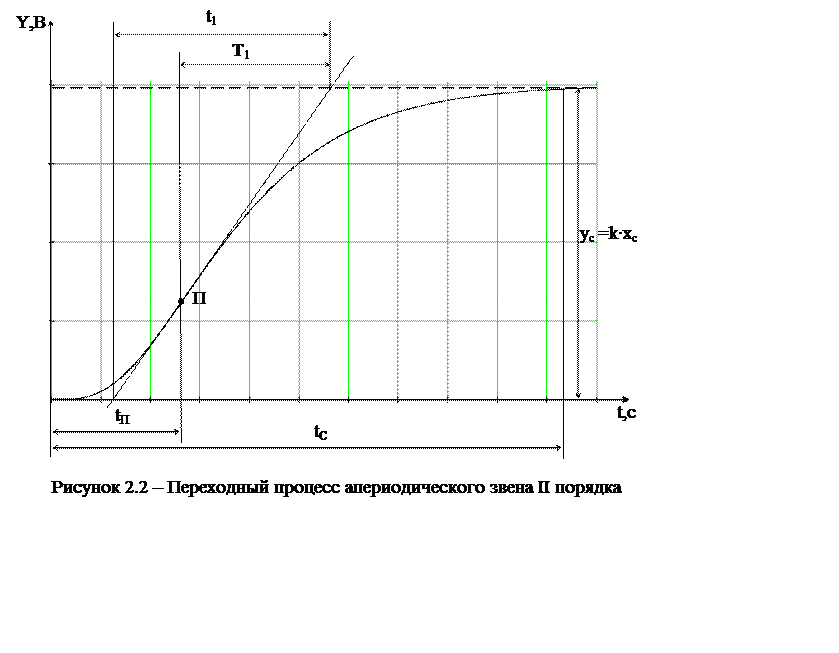
Переходная характеристика апериодического звена второго порядка представлена на рисунке 2.2. Проведем касательную к данной кривой в точке перегиба  П и отметим три отрезка времени t_п,  t₁, Т₁ ( см. рис. 2.2). Динамика апериодического  звена второго порядка описывается дифференциальным уравнением второго порядка :

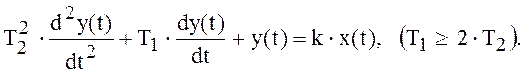 ,                    (2.8)

причем Т₁ берется непосредственно из графика переходной характеристики  y(t) (см рис. 2.2),  а величина  определяется специальными параметрическими  графиками на рисунках  2.3 и 2.4, в зависимости от t₁ и Т₁.  То же самое уравнение (2.8) записывается также еще в другом виде :

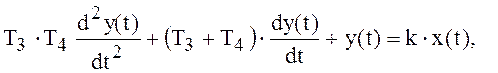                     (2.9)

что совпадает с уравнением (2.9), если принять обозначения :

.

Как видно, динамика  звена второго порядка определяется двумя постоянными времени  Т₁ и Т₂, причем , так как при этом корни характеристического уравнения 

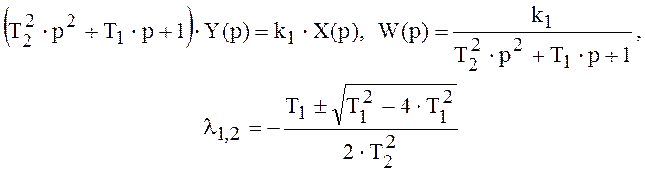
будут вещественными. передаточную функцию апериодического звена второго порядка по уравнению вида (2.9), разложив знаменатель на сомножители, можно записать в виде :

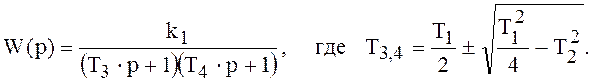
Кроме того, Т₃ и Т₄ можно определить из специального графика (рис.2.3), в зависимости от измеренных на кривой переходной характеристики величин t₁ и Т₁. На том же графике еще показана зависимость t_п  от t₁ и Т₁. Эта величина t_п   дана для целей проверки. В самом деле, на кривой  бывает трудно с достаточной точностью найти точку перегиба П и провести в ней касательную. Проделав это по возможности точно, надо затем после взятия с чертежа размеров t₁ и Т₁ убедиться в том, что на графике 2.3 для этих данных получается значение t_п  примерно такое же, как на кривой y(t). В противном случае надо заново провести построение  касательной, добившись примерного совпадения этих значений t_п .

Переходная характеристика апериодического звена второго порядка (рис.2.2), математически являющаяся решением дифференциального уравнения (2.8) или (2.9), записывается в виде :

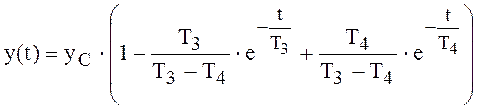.                            (2.10)

Это – сумма двух экспонент с разными постоянными времени Т₃ и Т₄ . Эти корни и стоят в показателях двух слагаемых экспонент в выражении переходной характеристики (2.10), точно так же как корень (2.5) стоял в показателе экспоненты апериодического звена первого порядка. Примерами такого звена являются двигатель постоянного тока при учете инерционности цепи якоря, электромашинный усилитель.

2.1.3 Колебательное  звено второго порядка и его параметры

Колебательное звено обладает колебательной переходной характеристикой, показанной на рисунке 2.5. Амплитуда колебаний затухает по экспоненте (пунктирные линии на рисунке 2.5). По графику переходной характеристики y(t) можно определить постоянную времени Т этой экспоненты (по двум-трем точкам верхней и нижней экспонент). Кроме того, на том же графике определяют полупериод колебаний t₁. По отношению этих двух величин Т/t₁ на основании специального графика (см. рис. 2.6) находят величину Т и вычисляют : 

Это дает возможность записать дифференциальное уравнение колебательного звена :

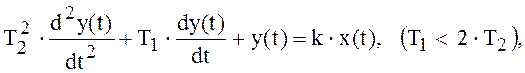           (2.11)

 

 

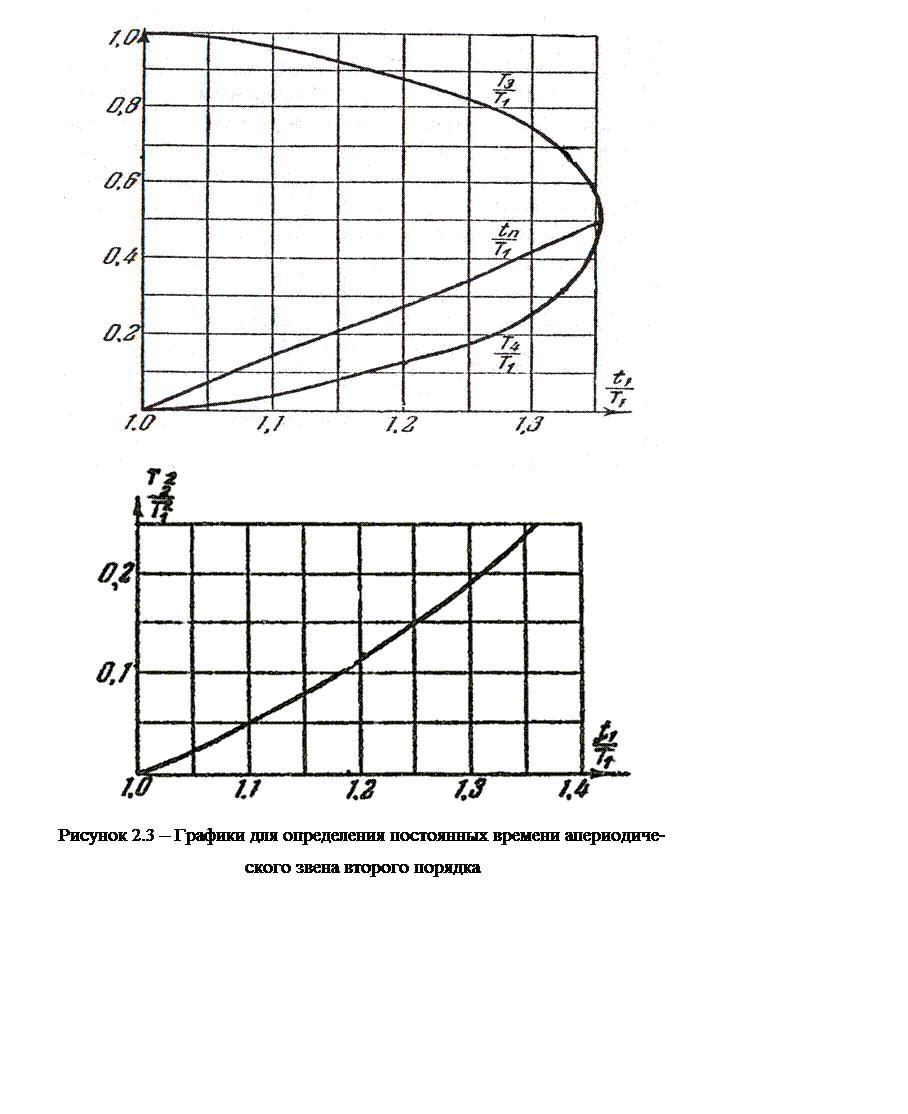
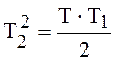
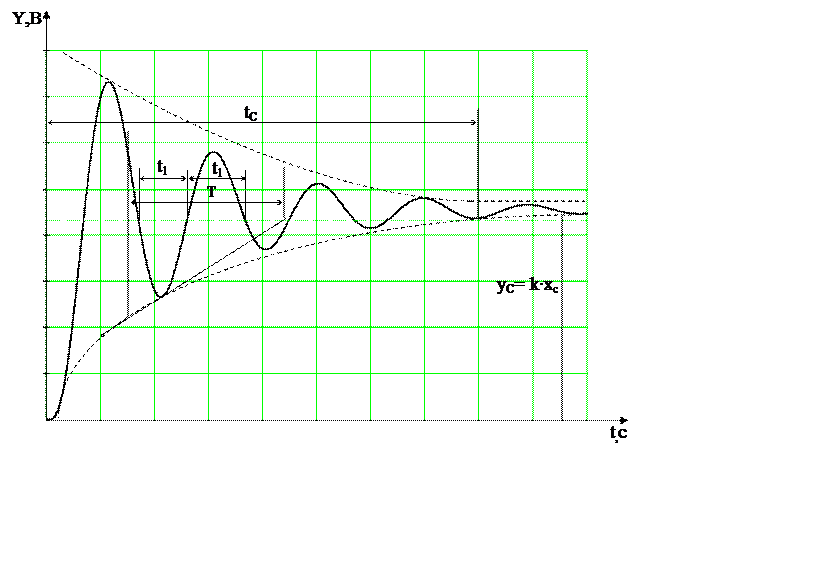
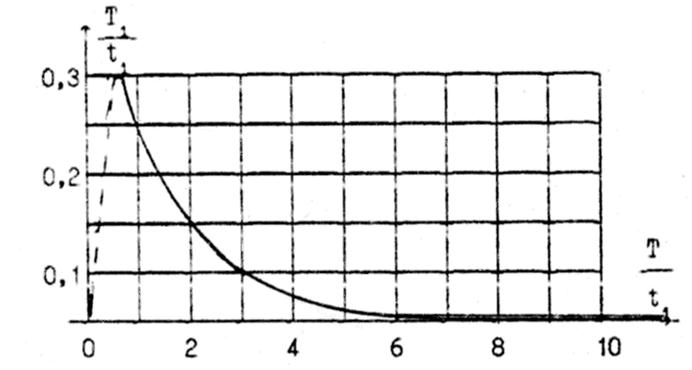Рисунок 2.5 - Переходная характеристика колебательного звена

Рисунок 2.6 – График для определения параметров колебательного звена

которое является уравнением второго порядка того же вида, что и уравнение (2.8), с той только разницей,  что здесь соотношение между постоянными времени Т₁  и Т₂  иное, а именно : Т₁ < 2 ·Т₂ . Следовательно, соотношение этих двух постоянных имеет определенный физический смысл  –  постоянная Т₁ характеризует собой демпфирование (сглаживание) собственных колебаний звена, а постоянная Т₂ – их раскачивание.

при этом корни характеристического уравнения 

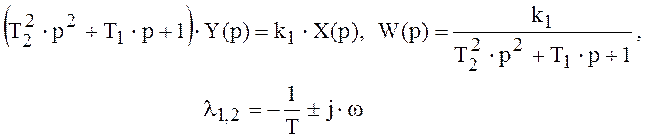
будут комплексными, чем и объясняется, математически, колебательное решение дифференциального уравнения вида (2.11) вместо апериодического (2.10), которому соответствовали вещественные корни. Общепринята запись передаточной функции колебательного звена в виде :

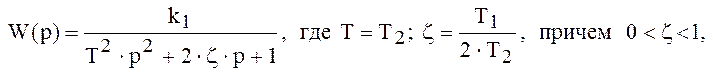
так как при звено становится апериодическим (второго порядка).

Формула для переходной характеристики колебательного звена (см. рис. 2.5) как решение уравнения (2.11) имеет вид :

,

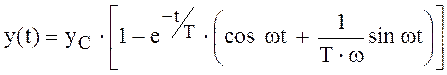где Т – постоянная времени затухания амплитуды колебаний;

          ω – частота колебаний, причем :

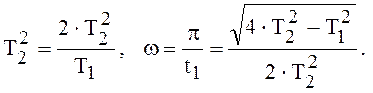
Время затухания колебаний будет tс ≈ 3∙Т. При отсутствии демпфирования  (Т₁ =0) дифференциальное уравнение колебательного звена (2.11) получит вид :

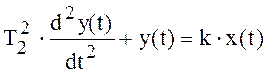 ,                                          (2.12)

и переходная характеристика выразится в форме незатухающих колебаний с постоянной амплитудой (см. рис.2.7), которые, в отличие от затухающих колебаний (см. рис.2.5), называются периодическими колебаниями :

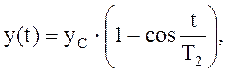
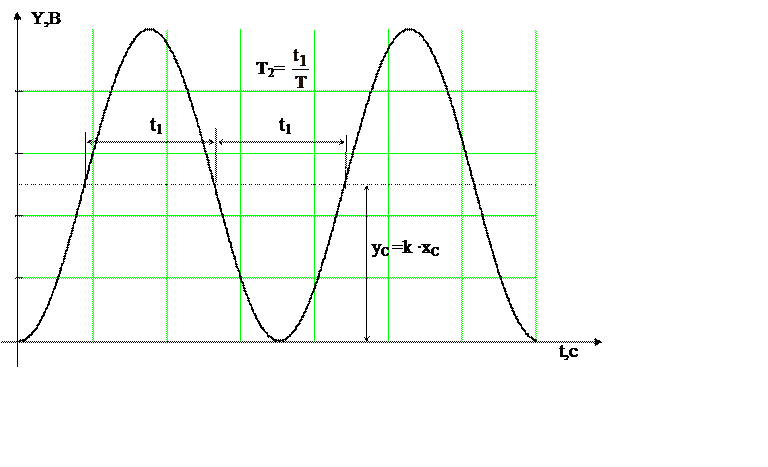причем характеристическое уравнение вида  будет иметь чисто мнимые корни :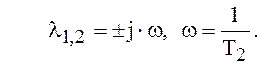

Рисунок 2.7 – Переходная характеристика консервативного звена