Методы исследования типовых звеньев ТАУ и систем в целом на базе аналоговых вычислительных машин с помощью типовых воздействий, переходных процессов и частотных характеристик САУ, страница 5

параметры	№ варианта
	1	2	3	4	5	6	7	8
UВХ, В	5	10	15	20	25	30	35	40
RBX, МОм	0.2	0.4	0.6	0.7	0.5	0.9	0.6	0.8
ROC, МОм	1.2	0.8	0.2	1.0	0.3	0.2	0.3	1.0

5 Проделав аналогичные операции (пп.1-4), получить выходную характеристику для затухающего экспоненциального внешнего воздействия по рисунку 1.2 и таблице 1.2, сравнив экспериментально снятую кривую  с теоретической, полученной по зависимости  :

U_вых=                                                   (1.4)

          где А= а ·100 В – значение начальных условий , взятых из таблицы 1.2;

       α – переменный коэффициент усиления интегратора (табл.1.2).

6 Проделав аналогичные операции (пп.1-4), получить выходную характеристику для гармонического синусоидального  внешнего воздействия по рисунку 1.3 и таблице 1.3, сравнив экспериментально снятую кривую  с теоретической, полученной по зависимости (1.2) :

7 В соответствие с изложенными выше требованиями составьте отчет по лабораторной работе и подготовьтесь к его защите, ответив на ниже следующие  контрольные вопросы.

 

Рисунок 1.2 – Схема набора и выходная характеристика

затухающего экспоненциального воздействия

Таблица 1.2 – Параметры для модели экспоненциальной характеристики

параметры	№ варианта
	1	2	3	4	5	6	7	8
A	0.2	-0.3	0.4	-0.45	0.5	-0.1	0.25	0.6
α	0.2	0.8	0.6	1.0	0.3	0.4	0.7	0.5

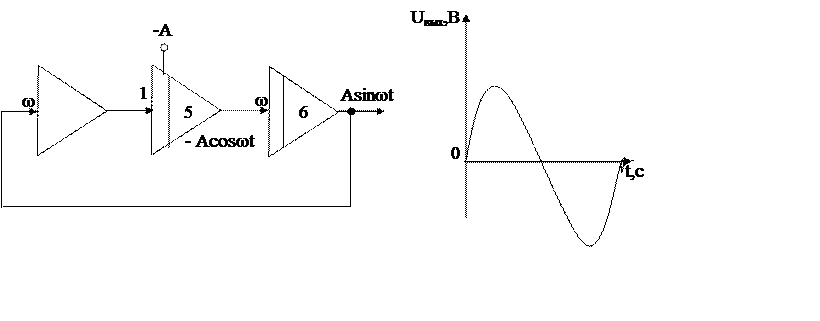
Рисунок 1.3 – Схема набора и график гармонического  синусоидального сигнала

Таблица 1.3 – Параметры для модели синусоидального сигнала

параметры	№ варианта
	1	2	3	4	5	6	7	8
Xm, В	20	10	25	50	35	40	45	35
ω,с –1	0.5	0.2	0.7	1	1.5	0.6	0.8	0.4

Контрольные вопросы

1 Чем отличаются электронные модели единичного ступенчатого и гармонического воздействий ?

2 Как регулировать параметры схемы электронной модели, чтобы получить многовариантность выходных характеристик ?

3  Что называют единичным ступенчатым воздействием ?

4 Приведите математическую модель графика  единичного ступенчатого воздействия ?

5 Для чего нужен генератор гармонического сигнала ?

6 Как влияет полярность ненулевых начальных условий на вид экспоненциальной входной характеристики  ?

7 Как из схемы генератора гармонического сигнала получить косинусоидальный гармонический сигнал ?

8 Как влияет величина коэффициента усиления на крутизну экспоненты  ?

9 Как изменить полярность любого внешнего воздействия ?

10 Какие виды внешних  воздействий Вы знаете, приведите их аналитическое описание.

II  ЛАБОРАТОРНАЯ РАБОТА 2

Исследование динамических свойств моделей типовых звеньев CАУ по временным характеристикам

Цель работы – изучение динамических характеристик типовых звеньев САУ по экспериментально полученным переходным характеристикам их электронных моделей.

2.1  Переходные характеристики типовых позиционных звеньев

2.1.1 Апериодическое звено первого порядка и его параметры

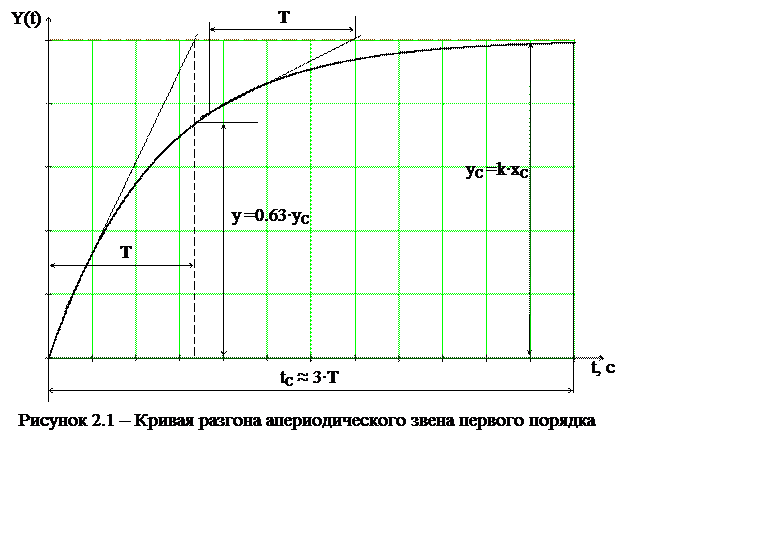
Знакомство с правилами определения количественных значений коэффициента усиления и постоянных времени следует начать с апериодического звена первого порядка. Переходная характеристика его  показана на рисунке 2.1. Математически эта кривая  описывается показательной функцией, которая называется экспонентой :

                                                  ,                                        (2.1)

          где Y_с – установившееся значение выходной величины Y, причем согласно статической характеристике Y_с= k·Х_с.

          Величина Т называется постоянной времени апериодического звена и имеет размерность [с]. Она определяется на графике переходной характе-ристики, как величина проекции касательной на линию установившегося значения y=y_с (см. рис. 2.1), причем во всех точках кривой она одинакова. Так как касательные к экспериментально полученной кривой y(t) проводить точно бывает трудно, то можно взять две-три точки кривой (как на рис. 2.1), найти для каждой из них величину Т и выбрать какое-то среднее ее значение. Кроме того, для уточнения этого значения надо использовать следующее свойство кривой (2.1) : в точке t = Т переменная y должна иметь значение  y =0.63·yс.

 

Таким образом, имея из опыта переходную характеристику апериодического звена первого порядка, можно определить его постоянную времени Т, и наоборот, если известна постоянная времени звена Т, то можно по формуле (2.1) построить его переходную характеристику. Из рисунка 2.1 видно, что чем больше постоянная времени Т, тем более полого пройдет кривая y(t), т.е. тем длительнее будет переходный процесс установления выходной величины yс . Поэтому говорят, что постоянная времени Т апериодического звена характеризует его инерционность (инерционное запаздывание в передаче входного сигнала на выход звена). Длительность переходного процесса будет :

t_c ≈ (3 ÷4 ) ∙Т, [с]                                                  (2.2)

(согласно формуле (2.2) кривая приближается к значению y_с асимптотически т.е. только при t=∞, но практически уже за время t ≈ 3∙Т эта кривая уже сливается с прямой y =y_с). Апериодическое звено характеризуется двумя числовыми данными :

коэффициентом усиления или передаточным числом k, определяющим статические свойства звена; постоянной времени Т, определяющей динамические свойства звена.