Методы исследования типовых звеньев ТАУ и систем в целом на базе аналоговых вычислительных машин с помощью типовых воздействий, переходных процессов и частотных характеристик САУ, страница 7

2.2.1 Параметры идеального интегрирующего звена

          Идеальное интегрирующее звено представляет собой такое устройство, у которого выходная величина пропорциональна интегралу от входной величины по времени, т.е. :

,                                         (2.13)

или, что то же самое, производная от выходной величины по времени пропорциональна входной величине :

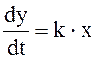                                               .                                                   (2.14)

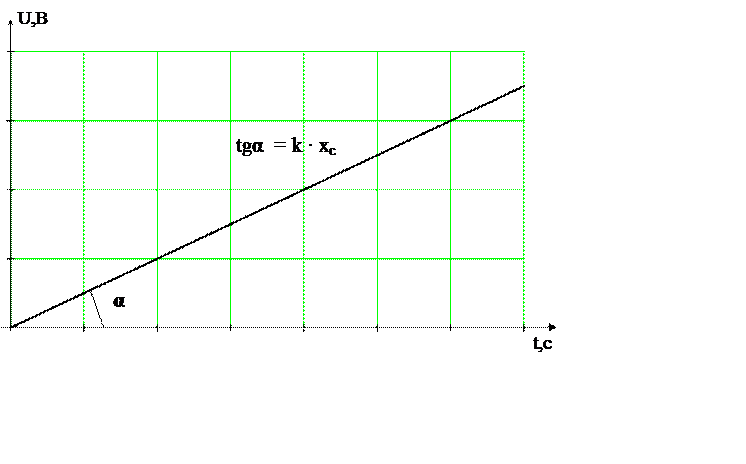
     Переходной характеристикой идеального интегрирующего звена согласно (2.13) будет наклонная прямая y(t) (см. рисунок 2.8), так как интеграл геометрически представляет собой площадь под кривой х(t), а в данном случае (х=const=х_с) эта площадь возрастает пропорционально абсциссе t :

                                      .                                                     (2.15)

Рисунок 2.8 – Переходная функция интегрирующего звена

2.3 Порядок выполнения работы на АВМ

1 Переключите на блоке питания  тумблер "Сеть" в положение "Вкл.", а через  две минуты - тумблер "Анод" в положение "Вкл". Подайте на решающий блок аналоговой машины постоянное напряжение 26 В.

2 После прогрева машины (15 мин.) настройте "нули" задействованных в задании усилителей (согласно приведенному выше описанию действий).   3 Произведите с помощью коммутационных проводов и наборного поля  АВМ набор схемы и отладку параметров моделей типовых звеньев  в соответствие с выданным  преподавателем заданием.

3.1 Схема набора и параметры апериодического звена первого порядка представлены на рисунке 2.9 и в таблице  2.1 соответственно.

 

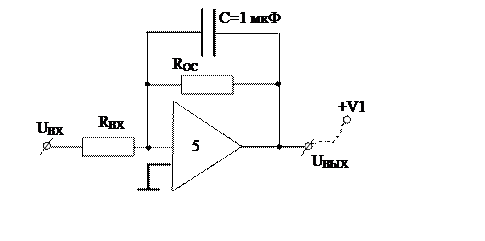Рисунок 2.9 – Схема модели апериодического звена первого порядка

Таблица 2.2 – Параметры апериодического звена первого порядка

параметры	№ варианта
	1	2	3	4	5	6	7	8
UВХ, В	5	10	15	20	25	30	35	40
RBX, МОм	0.2	0.4	0.6	0.7	0.5	0.9	0.6	0.8
ROC, МОм	1.2	0.8	0.2	1.0	0.3	0.2	0.3	1.0

3.2 Схема набора звена второго порядка представлены на рисунке 2.10. Параметры звена второго порядка и его тип (апериодическое второго порядка, колебательное, консервативное) задаются преподавателем в рабочем порядке.

3.3 Схема набора и параметры интегрирующего звена представлены на рисунке 2.12 и в таблице  2.3 соответственно.

 

Рисунок 2.10 – Схема модели звена второго порядка

 

Рисунок 2.11 – Схема модели интегрирующего  звена

Таблица 2.3 – Параметры интегрирующего звена

параметры	№ варианта
	1	2	3	4	5	6	7	8
UВХ, В	5	10	15	20	25	30	35	40
RBX, МОм	0.2	0.4	0.6	0.7	0.5	0.9	0.6	0.8

4 Получить переходную характеристику исследуемого звена (по указанию преподавателя),для чего нормировать кривую разгона путем деления ординат выходного напряжения исследуемого звена на входную величину.

5 Сравнить расчетную и экспериментальную переходные характеристики исследуемых звеньев.

6 Определить по экспериментальной переходной характеристике параметры, характеризующие статические и динамические свойства исследуемых звеньев. Сделать выводы о влиянии параметров звена на вид его  переходной характеристики.

Контрольные вопросы

1 Приведите дифференциальные уравнения звеньев первого и второго порядков.

2 Приведите уравнения переходных процессов звеньев первого и второго порядков.

3 Чем отличается кривая разгона от переходной характеристики, пояснить на примере.

4 Какими параметрами характеризуются динамические свойства  звеньев  второго порядка ?

5 Как определить постоянную времени колебательного звена ? 

6 Как изменится колебательное звено, если коэффициент демпфирования равен нулю ?

7 Какова размерность коэффициентов передачи и  постоянных времени ?   Пояснить методику их определения по переходным характеристикам исследуемых звеньев.

III Лабораторная работа  3

Исследование динамических свойств моделей типовых звеньев  систем автоматического управления по их частотным характеристикам

           Целью лабораторной работы является изучение экспериментального метода и аппаратных средств определения амплитудно-фазовых частотных  и динамических характеристик типовых звеньев.

Теоретические сведения

Для сложного объекта автоматического регулирования не всегда удается произвести исследование с помощью аналитических методов ввиду того, что заранее неизвестны математические модели, параметры объекта или существуют значительные нелинейности в объекте. В этом случае применим экспериментальный метод построения частотных характеристик исследуемого объекта, базирующийся на том, что если на его  вход подать сигнал синусоидальной формы с частотой ω и амплитудой, равной единице, то на выходе в установившемся режиме получится тоже синусоидальный сигнал с той же частотой ω но с другими амплитудой и фазой.

          Синусоидальные функции могут выражаться в векторной форме показательными функциями с мнимым аргументом :

W(jω) = А(ω)· φ(ω) = А(ω) ·е^{j· φ(ω)}  =  Р(ω) + j · Q(ω),                (3.1)

где е^{j· φ(ω)} = сos(ωt) +j · sin(ωt),

т.е. Р(ω)= А(ω) · сos(ωt), а Q(ω)= А(ω) · sin(ωt).

   где А(ω) – отношение амплитуд выходного и входного сигналов;

      φ(ω) – разность фаз выходного и входного сигналов.

Величина W(jω) называется комплексным коэффициентом передачи или усиления, представляющим комплексное число, модуль которого равен отношению  амплитуд выходного и входного сигналов при неизменной частоте ω входного сигнала. Если положить ω=0, то получается коэффициент усиления или коэффициент передачи системы или звена.