Расчет цепочечного полиномиального фильтра Чебышева. Расчет полиномиального фильтра Баттерворта

Содержание.

1. Введение.

2. Расчет полиномиального фильтра Чебышева.

2.1.  Определение передаточной функции фильтра.

2.2.  Составление схемы и расчёт параметров элементов фильтра.

2.3.  Расчёт частотных зависимостей затухания и фазового сдвига    полузвеньев фильтра.

2.4.  Расчёт частотной зависимости входного сопротивления фильтра.

3. Расчёт корректора фазочастотной характеристики фильтра.

3.1.  Определение требуемой частотной характеристики фазового сдвига корректора.

3.2.  Выбор схемы корректора и расчёт параметров его элементов.

3.3.  Расчёт частотных характеристик параметров передачи корректора и     суммарной результирующей характеристики тракта передач.

3.4.  Проверка соответствия полученных характеристик заданным допускам.

4. Схема тракта передачи.

5.  Дополнительное задание: «Расчёт полиномиального фильтра

   Баттерворта».

5.1.  Введение.

5.2.  Определение передаточной функции фильтра.

5.3.  Составление схемы и расчёт параметров элементов фильтра.

5.4.  Расчёт частотных зависимостей затухания и фазового сдвига    полузвеньев фильтра.

5.5.  Расчёт частотной зависимости входного сопротивления фильтра.

6. Приложение (графики частотных зависимостей).

7. Используемая литература.

1.  Введение.

В любой системе телемеханики и связи можно выделить, по крайней мере, две основные части: устройства сбора и распределения информации и устройства передачи её на расстояние.

 Указанные устройства должны  обеспечивать передачу по любым линиям связи (проводным, радио или смешанным) заданного количества информации с заданной верностью в условиях подверженности искажениям и помехам. Обе эти задачи (передача необходимого количества информации и обеспечение её верности) решают  использованием в передающих устройствах сигналов специальной формы и применением в приёмниках специальных устройств, восстанавливающих по возможности переданные сигналы обработкой принятых. Как при формировании сигналов в передающих устройствах, так и при восстановлении их в приёмных используются специальные аналоговые электрические цепи с соответствующими характеристиками.

В широком смысле любые устройства, преобразующие электрические сигналы, называют фильтрами. Электрические цепи, используемые для получения сигналов определённой формы, называют формирующими фильтрами. Цепи, наилучшим образом восстанавливающие сигналы в приёмных устройствах, называют оптимальными фильтрами.

Для отделения сигналов друг от друга или помех в тех случаях, когда и те, и другие содержат частотные составляющие, занимающие непрерывающиеся полосы частот, используют частотные фильтры.

В данной работе производится расчёт цепочечного полиномиального фильтра Чебышева. Цепочечные фильтры отличаются от простейших фильтрующих цепей более качественными частотными характеристиками.

Аппроксимация передаточной функции фильтра посредством полиномов Чебышева дает колебательный характер функции с равными отклонениями в полосе пропускания и монотонной – в полосе задерживания. Из всех полиномиальных фильтров с передаточными функциями равных порядков и одинаковой допустимой неравномерностью затухания в полосе пропускания максимальное затухание при любой частоте полосы задерживания имеют фильтры с характеристиками Чебышева. Однако фильтры Чебышева имеют более нелинейную фазовую характеристику в полосе пропускания  по сравнению с другими фильтами.

2.  Расчет полиномиального фильтра Чебышева

2.1. Определение передаточной функции фильтра.

Определим передаточную функцию фильтра. Квадрат модуля функции передачи фильтра Чебышева определяется выражением:

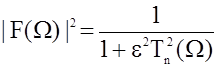Где  W - нормированная частота; W = f/f_ср;

T²_n(W) – полином Чебышева; его вид зависит от порядка фильтра n;

e - коэффициент неравномерности.

Коэффициент неравномерности e может быть найден по значению a_max (наибольшее затухание фильтра в полосе пропускания), если воспользоваться формулой:

   

Согласно исходным данным наибольшее затухание фильтра в полосе пропускания a_max = 0,5.Тогда получим следующеезначениекоэффициента неравномерности:

e = 0,349

Порядок фильтра  n определяется по формуле:

 

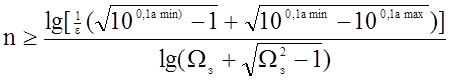где  W - нормированная частота; W = f/f_ср;

e - коэффициент неравномерности;

a_max – наибольшее затухание фильтра в полосе пропускания;

a_min – минимально допустимое затухание фильтра в полосе задерживания             фильтра на частоте W_з = f_з/f_ср .

Найдём порядок фильтра, подставив в формулу следующие значения:

e = 0,349, a_max = 0,5 дБ, a_min = 38 дБ, f_з = 2f_ср. Тогда:

 

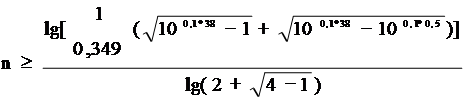Полученное значение n округляется до ближайшего целого числа в большую сторону. Следовательно получаем :