Другие предметы \ Теория передачи сигналов

Расчет цепочечного полиномиального фильтра Чебышева. Расчет полиномиального фильтра Баттерворта, страница 8

f, Гц	a_р, дБ	b_р, град.
0	0	0
200	0	12,26
400	2,218E-14	24,54
600	6,403E-12	36,87
800	3,594E-10	49,26
1000	8,171E-09	61,73
1200	1,049E-07	74,31
1400	9,08E-07	87,03
1600	5,888E-06	99,91
1800	3,063E-05	112,9
2000	0,000133	126,3
2200	0,000508	139,9
2400	0,00171	153,8
2600	0,00526	168,2
2800	0,0148	183,1
3000	0,0389	198,7
3200	0,0954	215,3
3400	0,219	232,9
3600	0,474	251,9
3800	0,956	272,2
4000	1,775	293,5
4200	3	315
4600	6,60	354,0
5000	10,96	385,0
5400	15,40	408,9
5800	19,67	427,8
6200	23,69	443,3
6600	27,48	456,4
7000	31,06	467,5
7400	34,43	477,2
7600	36,06	481,6
8000	39,17	489,7
8400	42,14	496,9

5.5. Расчёт частотной зависимости входного сопротивления фильтра.

Частотные зависимости входного сопротивления полиномиальных фильтров дают возможность оценить степень согласованности фильтров с сопротивлением источника сигнала (генератора) R_г и сопротивлением нагрузки R_н.

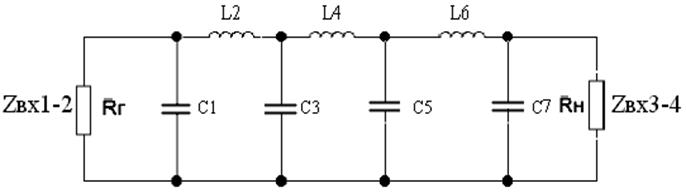Для схем,содержащих нечётное число элементов при R_г =R_н, входные сопротивления со стороны зажимов 1-2 и 3-4 равны (Z_{вх 1-2} = Z_{вх 3-4}). В этом случаи достаточно рассчитать одну из частотных зависимостей входного сопротивления Z_вх(f).

Рис. 7

Рассчитаем входное сопротивление фильтра. Порядок фильтра n=7.

Запишем формулы для расчёта Z_вх:

Поскольку Z_вх(f) представляет собой комплексное сопротивление, зависящее от частоты, то рассчитываются частотные зависимости модуля входного сопротивления |Z_вх(f)| в Омах и угла входного сопротивления в градусах:

Расчёты удобно выполнять на ЭВМ. Результаты расчётов приведены в таблице 11, а графическое изображение частотных зависимостей в приложении на графике 4.

Таблица№ 11.

f,Гц	\|Zвх\|,Ом	j,град	f,Гц	\|Zвх\|,Ом	j,град
0	300	0	3400	211,8	-15,6
200	300	0,03	3600	161,5	-12,5
400	300,1	0,06	3800	116,3	6,2
600	300,3	0,07	4000	101,4	34,3
800	300,5	0,08	4200	133,3	63,0
1000	300,6	0,07	4400	193,4	76,7
1200	300,8	0,05	4600	268,7	82,8
1400	301,1	0,01	5000	467,5	87,8
1600	301,5	-0,05	5400	793,6	88,2
1800	302,8	-0,18	5800	1513,2	88,9
2000	303,3	-046	6200	4990	89
2200	304,6	-1	6600	5555	-89,9
2400	305,5	-2,11	7000	1963	-89,9
2600	304,4	-3,94	7400	1244	-89,9
2800	298,2	-6,67	7600	1063	-89,9
3000	282,6	-10,2	8000	834,7	-89,9
3200	254,1	-10,7	8400	695	-89,9

1 2 3 4 5 6 7 8

Скачать файл