Расчет цепочечного полиномиального фильтра Чебышева. Расчет полиномиального фильтра Баттерворта, страница 6

5. Схема тракта передачи.

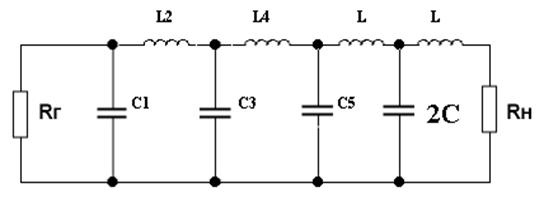Рис. 5

Таблица№ 7

Элемент	Значение
C1	0,215 мкФ
L2	13,99 мГн
C3	0,321 мкФ
L4	13,99 мГн
C5	0,215 мкФ
L	21,98 мГн
C	0,244 мкФ
Rн	300 Ом
Rг	300 Ом

5. Дополнительное задание: «Расчёт полиномиального фильтра Баттерворта».

         5.1. Введение.

    Фильтры Баттерворта – это фильтры с функцией передачи, построенной на основе функции Баттерворта. В общем случаи функция передачи ФНЧ имеет вид:                                                                                                                                                                                                                                                                                                                                                                                                             

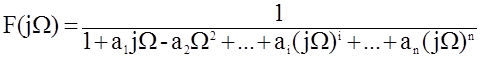Знаменатель представляет собой полином – многочлен Баттерворта. Многочлены Баттерворта приводятся в справочной литературе. Для данного фильтра многочлен Баттерворта выбирается в соответствии с порядком фильтра n. Определение вида функции передачи реальной электрической цепи с достаточной степенью точности, приближающейся к желаемой, называют аппроксимацией. Построение цепи по заданной реализуемой функции передачи F(jW) называют реализацией.

5.2.  Определение передаточной функции фильтра.

Определим передаточную функцию фильтра. Квадрат модуля функции передачи фильтра Баттерворта определяется выражением:

где  W - нормированная частота; W = f/f_ср;

k_2n = 1 при практическом использовании;

n – порядок фильтра (число элементов в схеме фильтра).

    Порядок фильтра n рассчитывается по следующей формуле

где а_min – минимально допустимое затухание фильтра в полосе задерживания фильтра на частоте W_з = f_з/f_ср

Рассчитаем порядок фильтра для заданных значений а_min  = 38дБ и f_з = 2f_ср:

W_з = 2f_ср/f_ср = 2

W_з =2

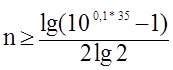Если расчётное значение n не целое, то за n принимается ближайшее большее целое число. Следовательно получаем:

n = 7

    Таким образом, квадрат модуля функции передачи имеет вид:

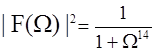Её значения при различных значениях W представлены в таблице 8, а график зависимости | F(W) |²  -  на графике 1 приложения.

Таблица№ 8.

W	|F(W)|^2	W	|F(W)|^2	W	|F(W)|^2
0	1	0,52380	0,99988	1,09523	0,21864
0,04761	1	0,57142	0,99960	1,19047	0,08010
0,09523	1	0,61904	0,99878	1,28571	0,02879
0,14285	1	0,66666	0,99658	1,38095	0,01078
0,19047	1	0,71428	0,99108	1,47619	0,00426
0,23809	1	0,76190	0,97826	1,57142	0,00178
0,28571	1	0,80952	0,95065	1,66666	0,00078
0,33333	0,99999	0,85714	0,89642	1,76190	0,00035
0,38095	0,99999	0,90476	0,80236	1,80952	0,00024
0,42857	0,99999	0,95238	0,66442	1,90476	0,00012
0,47619	0,99996	1	0,5	2	0,00006