Расчет цепочечного полиномиального фильтра Чебышева. Расчет полиномиального фильтра Баттерворта, страница 3

2.4. Расчёт частотной зависимости входного сопротивления фильтра.

Частотные зависимости входного сопротивления полиномиальных фильтров дают возможность оценить степень согласованности фильтров с сопротивлением источника сигнала (генератора) R_г и сопротивлением нагрузки R_н.

    Для схем,содержащих нечётное число элементов при R_г =R_н, входные сопротивления со стороны зажимов 1-2 и 3-4 равны (Z_{вх 1-2} = Z_{вх 3-4}; см. рис.2). В этом случаи достаточно рассчитать одну из частотных зависимостей входного сопротивления Z_вх(f). Для схем фильтров, содержащих чётное число элементов,      и рассчитываются оба входных сопротивления.

 

    Рассчитаем входное сопротивление фильтра. Порядок фильтра n=5,

следовательно Z_вх1-2 = Z_вх3-4 . Запишем формулы для расчёта Z_вх1-2 = Z_вх3-4 :

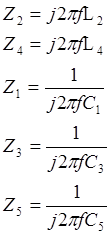
          Поскольку Z_вх(f) представляет собой комплексное сопротивление, зависящее от частоты, то рассчитываются частотные зависимости модуля входного сопротивления |Z_вх(f)| в Омах и угла входного сопротивления     в    градусах:

Расчёты удобно выполнять на ЭВМ. Результаты расчётов приведены в таблице 4, а графическое изображение частотных зависимостей

|Z_вх(f)|, приведено в приложении на графике 4.

Таблица №4.

f,Гц	|Zвх|,Ом	j,град	f,Гц	|Zвх|,Ом	j,град
0	300	0	3000	313,7	-28,8
200	290,47	-9,2	3200	277,2	-33,8
400	266,19	-16,6	3400	239,7	-34,2
600	235,87	-21,3	3600	213,8	-27,7
800	206,57	-23	3800	218,3	-13,6
1000	182,20	-21,5	4000	306,8	0,33
1200	164,98	-17,2	4200	585,9	-9,39
1400	156,72	-10,5	4400	700,98	-55
1600	159,17	-2,8	4600	479,1	-78,9
1800	173,71	3,9	4800	358	-85,6
2000	200,92	7,9	5000	292,8	-87,9
2200	239,7	7,7	5800	187,1	-89,8
2400	284,9	2,8	6400	153,5	-89,9
2600	322,4	-6,4	7000	131,9	-89,97
2800	333,6	-17,8	8400	104,73	-89,99

3.  Расчёт корректора фазочастотной характеристики фильтра.

 Фазочастотные корректоры включаются в тракты передачи сигналов для формирования линейной фазочастотной характеристики. При этом выравнивается и приближается к постоянному групповое время распространения сигналов.

3.1.  Определение требуемой частотной характеристики фазового сдвига корректора.

Задаёмся линейной характеристикой b_р=(1,1…1,4)b_{ф max}.

Определяем b_{к тр}=b_р-b_ф.

Частотные зависимости представлены в приложении на графике 5.

3.2.  Выбор схемы корректора и расчёт параметров его элементов.

Затухание корректора должно быть минимальным, а характеристическое сопротивление – постоянным, не зависящим от частоты. Этим условиям удовлетворяют симметричные мостовые схемы с реактивными взаимообратными сопротивлениями Z₁ и Z₂. Так как максимальное значение требуемого фазового сдвига корректора не превышает 180 градусов, то для построения корректора используем фазовый контур первого порядка (см. рис. 3).

L