Расчет цепочечного полиномиального фильтра Чебышева. Расчет полиномиального фильтра Баттерворта, страница 7

5.3.  Составление схемы и расчёт параметров элементов фильтра.

Выбор схемы зависит от стремления получить фильтр с наименьшим числом индуктивных элементов, или от заданных условий работы схемы. Учитывая, что нам необходимо получить ФНЧ, составим  цепочечную схему фильтра Баттерворта (рис. 6):

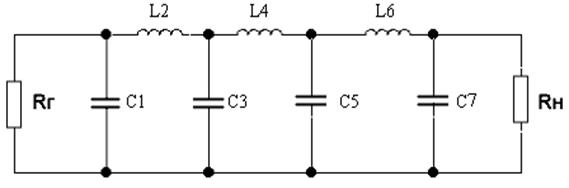Рис.6.

    Рассчитаем параметры элементов фильтра. Для этого необходимо преобразовать нормированные значения в реальные. Используем следующие формулы:

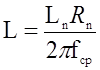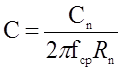где  L_н , C_н – нормированные значения;

R_н – сопротивление нагрузки.

Подставляя R_н = 300 Ом, f_ср = 4200 Гц и нормированные значения из справочной литературы (для L₂, L₄, L₆, C₁, C_7, C₃ и C₇ соответственно) получим следующие значения параметров элементов фильтра (таблица 9):

Таблица№ 9

Элемент	C1, мкФ	С3, мкФ	C5, мкФ	C7, мкФ	L2,Гн	L4,Гн	L6,Гн
Нормиро-ванное значение	1,737	2,638	2,638	1,737	1,258	1,344	1,258
Значения элементов фильтра	0,0561	0,227	0,227	0,0561	0,0142	0,0227	0,0142

5.4.  Расчёт частотных зависимостей затухания и фазового сдвига  полузвеньев фильтра.

Рабочее затухание фильтра а_р при аппроксимации Баттерворта на частоте среза постоянно для фильтров с любым числом элементов и равно:

    Рассчитаем частотную зависимость рабочего затухания фильтра Баттерворта. Для этого используем формулу:

Согласно исходным данным частота f_ср= 4200 Гц. Результаты расчёта  а_р приведены в таблице 10, а график частотной зависимости рабочего затухания- - на графике 2 приложения.

          Теперь произведём расчёт частотной зависимости рабочего фазового сдвига. Это можно сделать по следующей формуле:

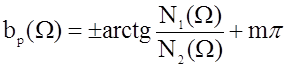Здесь: m= 0,1,2,...;

              

- сумма слагаемых нечётных степеней W

из многочлена Баттерворта;

                                                       

- сумма слагаемых чётных степеней W из из многочлена Баттерворта.

      Так как функция arctg(x) периодическая, значения        m подбираются так, чтобы фазовый сдвиг фильтра в глубине полосы пропускания достигал значений, а частотная характеристика b_р(W) была плавно изменяющейся во всём диапазоне частот.

Для ФНЧ  формула для расчёта частотнойзависимости рабочего фазового сдвига будет иметь вид:

    Рассчитаем частотную зависимость рабочего фазового сдвига, учитывая, что порядок фильтра n=7. Тогда получим следующие выражения для N₁(W) и N₂(W):

 

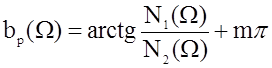Подставляя W = f/f_ср, где f_ср = 4200 получим частотную зависимость b_р(f). Результаты расчёта b_р приведены в таблице 10, а график частотной зависимости b_р(f) представлен  на графике 3 приложения .

Таблица№ 10