





























I. Расчетно-графическая работа по теме «Численные методы решения задачи Коши».
Пусть дана задача Коши: 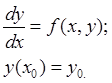
Построим приближенное решение задачи (1.1), определенное лишь в конечном числе
точек ![]() заданного отрезка
заданного отрезка ![]() .
.
Определение.
Множество точек ![]() , на котором ищется приближенное
решение называется сеткой. Точки
, на котором ищется приближенное
решение называется сеткой. Точки ![]() - узлы
сетки, величина
- узлы
сетки, величина ![]() - шаг сетки. Функция
дискретного аргумента
- шаг сетки. Функция
дискретного аргумента ![]() , определенная лишь в узлах сетки
называется сеточной функцией.
, определенная лишь в узлах сетки
называется сеточной функцией.
Для определения
сеточной функции ![]() , являющейся приближенным
решением исходной дифференциальной задачи (1.1), должна быть задана разностная
схема – система уравнений, связывающих между собой значения сеточной
функции
, являющейся приближенным
решением исходной дифференциальной задачи (1.1), должна быть задана разностная
схема – система уравнений, связывающих между собой значения сеточной
функции ![]() , заданных дополнительных условий и правой
части уравнения (1.1) в узлах
, заданных дополнительных условий и правой
части уравнения (1.1) в узлах ![]() .
.
Если исходную задачу можно записать в виде:
![]() ,
,
где L - дифференциальный оператор, то соответствующая разностная схема –
![]() ,
,
где ![]() - разностный оператор.
- разностный оператор.
Задача
определения сеточных функций ![]() должна быть поставлена
так, чтобы при
должна быть поставлена
так, чтобы при ![]() , сеточные функции сходились в
определенном смысле к точному решению дифференциальной задачи.
, сеточные функции сходились в
определенном смысле к точному решению дифференциальной задачи.
Определение.
Будем говорить, что семейство сеточных функций ![]() сходится
к точному решению
сходится
к точному решению ![]() задачи (1.2), если
задачи (1.2), если ![]() .
.
Если,
кроме того, существует такое ![]() , что при
, что при ![]()
![]() ,
,
где C, k - постоянные величины, не зависящие от h, то будем говорить, что имеет место сходимость порядка k.
Сеточная функция ![]() и решение
дифференциального уравнения (1.2) - y(x) удовлетворяют
уравнениям разной природы. Поэтому для оценки близости решения разностной
задачи (1.3) к решению дифференциального уравнения (1.2) используют понятия
«аппроксимация» и «устойчивость» разностной схемы.
и решение
дифференциального уравнения (1.2) - y(x) удовлетворяют
уравнениям разной природы. Поэтому для оценки близости решения разностной
задачи (1.3) к решению дифференциального уравнения (1.2) используют понятия
«аппроксимация» и «устойчивость» разностной схемы.
Определение.
Будем говорить, что разностная схема имеет k-ый
порядок аппроксимации на решении задачи (1.2), если существует такое ![]() , что при
, что при ![]()
![]()
где где C, k - постоянные величины, не зависящие от h.
Определение.
Схема называется устойчивой по начальным условиям и правой части
уравнения, если существует такое ![]() , что
при
, что
при ![]() для нормы погрешности выполняется
неравенство
для нормы погрешности выполняется
неравенство
![]() ,
,
т.е. малое изменение исходных данных приводит к малому изменению решения.
Связь аппроксимации и устойчивости со сходимостью определяет теорема [4].
Теорема.
Если разностная схема (1.3) устойчива и аппроксимирует задачу (1.2) с порядком k, то решение ![]() при
при ![]() ,
сходится к решению
,
сходится к решению ![]() , причем порядок сходимости тоже
равен k, т.е. имеет место
оценка (1.5).
, причем порядок сходимости тоже
равен k, т.е. имеет место
оценка (1.5).
Методы Рунге-Кутты.
Пусть функция ![]() в уравнении (1.1) имеет
непрерывные частные производные вплоть до
в уравнении (1.1) имеет
непрерывные частные производные вплоть до ![]() -го
порядка. Тогда решение уравнения (1.1) будет иметь непрерывные частные
производные вплоть до
-го
порядка. Тогда решение уравнения (1.1) будет иметь непрерывные частные
производные вплоть до ![]() -го порядка:
-го порядка:
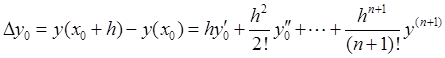 .
.
Все производные в правой части формулы (1.8) можно вычислить с помощью уравнения (1.1). Будем искать численное решение (1.1) в виде:
![]() ,
,
где ![]() - постоянные коэффициенты,
- постоянные коэффициенты, ![]() ,
, ![]() -
коэффициенты,
-
коэффициенты, ![]() - шаг дискретизации.
- шаг дискретизации.
Выбрав
шаг ![]() , зная коэффициенты
, зная коэффициенты ![]() ,
,![]() , можно определить решение
, можно определить решение ![]() . Выбор коэффициентов
. Выбор коэффициентов ![]() ,
,![]() ,
производится таким образом, чтобы разложения (1.8) и (1.9) совпадали до
возможно более высоких степеней
,
производится таким образом, чтобы разложения (1.8) и (1.9) совпадали до
возможно более высоких степеней ![]() . Этим
условиям удовлетворяет метод Рунге-Кутты второго порядка:
. Этим
условиям удовлетворяет метод Рунге-Кутты второго порядка:
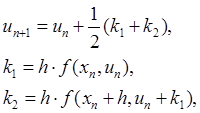
со вторым порядком аппроксимации и формулы Рунге-Кутты четвертого порядка:
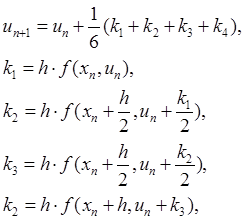
с четвертым порядком аппроксимации.
Анализ устойчивости схем Рунге-Кутты.
В общем виде схемы Рунге-Кутты можно записать:
![]() , где
, где ![]() - некоторая непрерывная функция аргумента
- некоторая непрерывная функция аргумента ![]() . Уравнение (1.10) будет устойчивым, если
устойчиво соответствующее однородное уравнение:
. Уравнение (1.10) будет устойчивым, если
устойчиво соответствующее однородное уравнение:
![]() .
.
![]()
Исследование на устойчивость разностного уравнения (1.11) эквивалентно исследованию на устойчивость дифференциального модельного уравнения [1]:
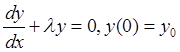 .
.
Для
схемы Рунге-Кутты второго порядка 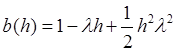 при решении модельного
уравнения, а так как схема будет устойчива при условии
при решении модельного
уравнения, а так как схема будет устойчива при условии ![]() ,
т.е., если
,
т.е., если ![]() , то выполнение условия эквивалентно
ограничению на выбор шага:
, то выполнение условия эквивалентно
ограничению на выбор шага: ![]() .
.
Для
схемы Рунге-Кутты четвертого порядка условие устойчивости несколько слабее: ![]() . Данные схемы условно устойчивы, но
выбор шага
. Данные схемы условно устойчивы, но
выбор шага ![]() позволяет их использовать при решении
различных классов задач. Все методы Рунге-Кутты являются явными, т.е.
вычисления
позволяет их использовать при решении
различных классов задач. Все методы Рунге-Кутты являются явными, т.е.
вычисления ![]() проводятся только при известных
проводятся только при известных ![]() и одношаговыми ( для определения
и одношаговыми ( для определения ![]() делается один шаг от
делается один шаг от ![]() к
к ![]() ).
).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.