![]() где
где ![]() - погрешность.
- погрешность.
Формула
(1.14) предполагается точной для многочленов до четвертой степени, т.е. при ![]() . Используя эти пять условий, и выбрав два
коэффициента в качестве параметров (например,
. Используя эти пять условий, и выбрав два
коэффициента в качестве параметров (например, ![]() ),
получаем следующие выражения для определения остальных коэффициентов:
),
получаем следующие выражения для определения остальных коэффициентов:
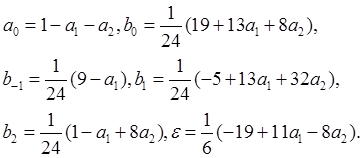
Для
построения формулы (1.14) мы использовали разложение функции y(x) в ряд Тейлора вплоть до пятого члена. Поэтому
порядок аппроксимации для данной формулы будет в общем случае ![]() , а погрешность
, а погрешность ![]() .Выбором
параметров
.Выбором
параметров ![]() мы можем попробовать повысить порядок
аппроксимации, а можем использовать эти параметры для увеличения устойчивости
формулы (1.14).
мы можем попробовать повысить порядок
аппроксимации, а можем использовать эти параметры для увеличения устойчивости
формулы (1.14).
Исследуем
формулу (1.14) на устойчивость. Пусть y(x) –
точное решение уравнения (1.1). Тогда ![]()
![]()
где ![]() - погрешность, возникающая при подстановке
точного решения в неточную формулу (1.14). Определим погрешность разностной
схемы (1.14) следующим образом:
- погрешность, возникающая при подстановке
точного решения в неточную формулу (1.14). Определим погрешность разностной
схемы (1.14) следующим образом: ![]() , вычитая из соотношения
(1.15) соотношение (1.14), получим разностное уравнение для вычисления
погрешности.
, вычитая из соотношения
(1.15) соотношение (1.14), получим разностное уравнение для вычисления
погрешности.
![]()
Значение
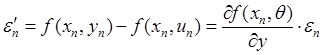 по теореме о среднем, где
по теореме о среднем, где ![]() . Так как шаг интегрирования h достаточно мал, то можно предположить, что величины
. Так как шаг интегрирования h достаточно мал, то можно предположить, что величины ![]() и
и 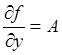 -
постоянны (на практике они обычно медленно меняются от шага к шагу). С учетом
этих допущений выражение (1.16) примет вид:
-
постоянны (на практике они обычно медленно меняются от шага к шагу). С учетом
этих допущений выражение (1.16) примет вид:
![]()
Соотношение (1.17) – это линейное разностное уравнение. Так как в уравнении (1.17) величины A и h встречаются только в виде произведения, то естественно считать, что выбор шага h может компенсировать влияние коэффициента A.Устойчивость разностного уравнения (1.17) обеспечивается устойчивостью соответствующего однородного разностного уравнения. Общее решение однородного разностного уравнения имеет вид:
![]() .
.
Т.е.
решение, полученное по формуле (1.14) будет устойчивым и ошибка ![]()
не будет
возрастать, если ![]() и будет условно устойчивым,
если
и будет условно устойчивым,
если ![]() . В некоторых случаях выбор параметров
. В некоторых случаях выбор параметров ![]() позволяет построить устойчивую коррекцию.
позволяет построить устойчивую коррекцию.
Общий вид линейного прогноза по трем точкам [1]:
![]()
Будем
определять коэффициенты прогноза (1.18) исходя из погрешности аппроксимации
порядка ![]() . Это означает, что формула (1.18) будет
точной для полиномов степени не выше третьей, т.е. мы получаем следующее
семейство прогнозов:
. Это означает, что формула (1.18) будет
точной для полиномов степени не выше третьей, т.е. мы получаем следующее
семейство прогнозов:
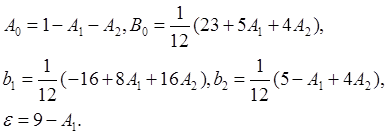
Исследование на устойчивость проводится так же как и для коррекции.
Определение.
Прогнозами (коррекциями) типа Милна называются прогнозы (коррекции),
использующие дополнительные «старые» значения функции, например, ![]() .
.
Прогнозами
(коррекциями) типа Адамса-Башфорта называются прогнозы (коррекции),
использующие дополнительные «старые» значения производной, например, ![]() .
.
План выполнения расчетно-графической работы.
1. Для заданного уравнения прогноза (коррекции) выбрать порядок аппроксимации. В соответствии с выбранным порядком аппроксимации вычислить коэффициенты прогноза (коррекции) и определить некоторое семейство прогнозов (коррекций).
2. Исследовать полученное семейство на устойчивость. Определить область абсолютной (условной) устойчивости в зависимости от коэффициентов исследуемого разностного уравнения.
3. Для заданного уравнения прогноза (коррекции) определить соответствующее уравнение коррекции (прогноза). Вычислить коэффициенты этого уравнения и исследовать его на устойчивость.
4. Из полученного семейства «прогноз-коррекция» выделить две пары прогнозов и коррекций (это минимальное количество исследуемых схем) и провести ряд вычислительных экспериментов.
5. Проанализировать результаты вычислительных экспериментов, сделать выводы.
Вычислительные эксперименты предлагается проводить следующим образом:
1. Выбрать шаг h, при котором теоретически выполняется неравенство (1.5) (обычно на практике шаг h<0,1).
2.
Для заданных тестов получить численное решение методами
«прогноз-коррекция» на отрезке [0,1] с шагом ![]() . Так как методы «прогноз-коррекция» не
самоначинающиеся, то первые несколько значений решения вычисляются с помощью
методов Рунге-Кутты.
. Так как методы «прогноз-коррекция» не
самоначинающиеся, то первые несколько значений решения вычисляются с помощью
методов Рунге-Кутты.
3. Полученные результаты оформить в виде таблицы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.