Расчетно-графическая работа по теме «Численные методы решения задачи Коши», страница 5

29. Исследовать семейство трехточечных прогнозов по Адамсу-Башфорту и двухточечных коррекций по Милну. Выбрать максимально устойчивую пару «прогноз-коррекция». Обосновать выбор.

30. Исследовать семейство трехточечных прогнозов и коррекций, построенных как линейная комбинация прогнозов и коррекций типа Милна и типа Адамса-Башфорта. Выбрать максимально устойчивую пару «прогноз-коррекция». Обосновать выбор.

Тестовые задачи.

1. 

2. 

3.

II.  Лабораторные работы по курсу «Дифференциальные уравнения».

Лабораторная работа №1. Численные методы решения систем дифференциальных уравнений.

Цель работы: Разработать программно-алгоритмическое обеспечение для решения жестких систем дифференциальных уравнений.

Исследовать разработанные алгоритмы на тестовых задачах.

Содержание работы: Многие методы решения обыкновенных дифференциальных уравнений (ОДУ) автоматически переносятся на системы обыкновенных дифференциальных уравнений (СОДУ):

                                                      

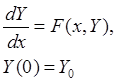
где - неизвестная вектор-функция;

 - заданная вектор-функция.

По теореме об устойчивости СОДУ по первому приближению [3] систему (2.1) можно представить в виде:

                                          

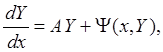
где A – постоянная матрица,  - правая часть порядка . Система (2.2) будет устойчива, если ,   - собственные значения матрицы A [3]. Многие практические задачи (задачи горения, термохимии) называются жесткими и решение этих задач представляет определенные трудности. Жесткие задачи – это задачи, в решении которых наряду с медленно меняющимися компонентами присутствуют и быстро меняющиеся компоненты. Сточки зрения свойств матрицы A жесткие задачи можно определить следующим образом [2].

Определение. Задачу (2.2) можно назвать жесткой, если:

1)  существуют , для которых ;

2)  существуют  умеренной величины, т.е.  «мал» по сравнению с абсолютными величинами собственных значений, удовлетворяющих пункту1;

3)  не существуют  с «большой» положительной вещественной частью;

4)  не существует  с «большой» мнимой частью, для которого не выполняется условие .

Если матрица A симметрична, то жесткость системы (2.2) означает, что система плохообусловлена [4].

Разностные схемы, соответствующие СОДУ (2.2) имеют вид [4]:

,                                         

.                                        

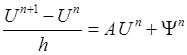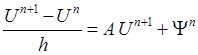Схемы (2.3) и (2.4) называются соответственно явной  и  неявной  двухслойной разностной схемой.

В общем случае двухслойная схема имеет вид:

.                                          

Погрешность аппроксимации определяется для систем ДУ так же как и для дифференциального  уравнения.

Если переписать схему (2.5) в каноническом виде:

,                                          

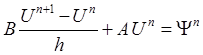то устойчивость соответствующей однородной системы определяется теоремой [4].

Теорема.  Если   - самосопряженный положительный оператор и существует оператор , то для устойчивости схемы (2.6) в Гильбертовом пространстве  с нормой  :  необходимо и достаточно, чтобы выполнялось неравенство:

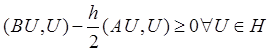
или

.                                                     

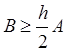Применение этой теоремы дает оценку шага явной схемы (2.3): .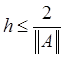

Т.е. при решении СОДУ с помощью явных схем требования к выбору шага интегрирования  предъявляются очень высокие (шаг интегрирования приходится выбирать очень мелкий).

Основной целью данной работы является исследование возможности применения явных и неявных двухслойных схем при решении нелинейных СОДУ и жестких СОДУ.

В качестве общей схемы решения ОДУ или СОДУ можно предложить следующий алгоритм:

Алгоритм решения СОДУ методами типа «пргноз-коррекция».

1.  Так как методы «прогноз-коррекция» не самоначинающиеся , то несколько первых шагов делают методом Эйлера (при невысокой требуемой точности) или методами Рунге-Кутты.

2.  Вычисление  и  .

3.  Вычисление .

4.  Если  , где   - заданная погрешность, то уменьшить шаг h в два раза и вернуться на 1. Если , то увеличить шаг h в два раза.