Порядок точности (погрешность вычислений) метода Рунге-Кутты можно оценить
следующим образом: пусть ![]() - точное решение
уравнения (1.1),
- точное решение
уравнения (1.1), ![]() - приближенное решение уравнения
(1.1). Обозначим
- приближенное решение уравнения
(1.1). Обозначим ![]() - решение, полученное по схеме
Рунге-Кутты с шагом
- решение, полученное по схеме
Рунге-Кутты с шагом ![]() ,
, ![]() - с
шагом
- с
шагом ![]() . Тогда:
. Тогда:
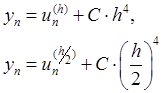
Вычитая из первого соотношения второе, получим погрешность метода Рунге-Кутты:
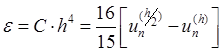 .
.
Соотношение (1.12) позволяет достаточно точно вычислять погрешность метода Рунге-Кутты. Недостатком этой оценки является необходимость дважды вычислять решение.
Методы прогноза и коррекции.
В общем случае для решения дифференциальной задачи (1.1) используются многошаговые разностные схемы:
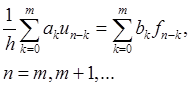 , где
, где ![]() - некоторые постоянные коэффициенты,
- некоторые постоянные коэффициенты, ![]()
Определение.
Схема (1.13) является явной (экстраполяционной), если ![]() и значения
и значения ![]() определяются
через предыдущие значения
определяются
через предыдущие значения ![]() ,
, ![]() ,…,
,…,![]() по
явной формуле:
по
явной формуле: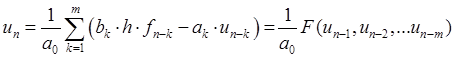 . Вычисления начинаются с n=m, т.е. для вычисления
. Вычисления начинаются с n=m, т.е. для вычисления ![]() необходимо
задать m начальных значений
необходимо
задать m начальных значений ![]() (методы Рунге-Кутты используют только одно
начальное значение
(методы Рунге-Кутты используют только одно
начальное значение ![]() ). Такие методы называются многошаговыми.
). Такие методы называются многошаговыми.
Если ![]() , то схема (1.13) называется неявной
(интерполяционной). В этом случае для определения
, то схема (1.13) называется неявной
(интерполяционной). В этом случае для определения ![]() для каждого n
необходимо решать нелинейное уравнение:
для каждого n
необходимо решать нелинейное уравнение: ![]() Это
нелинейное уравнение можно решать, например, методом Ньютона. Коэффициенты
Это
нелинейное уравнение можно решать, например, методом Ньютона. Коэффициенты ![]() подбирают исходя из требований
аппроксимации и устойчивости.
подбирают исходя из требований
аппроксимации и устойчивости.
Идеология построения методов “прогноз-коррекция”достаточно проста и основана на свойствах решения
дифференциального уравнения (1.1). Под решением уравнения (1.1) мы понимаем
кривую y(x), тангенс
угла наклона к которой в каждой точке (x , y) задается уравнением (1.1) - это локальное свойство.
Распространение этого локального свойства на всю область определения и означает
решение уравнения. Естественно, что решением уравнения (1.1) является не одна
кривая, а через любую точку ![]() проходит решение
уравнения (1.1).
проходит решение
уравнения (1.1).
Если мы хотим получить единственное решение, проходящее через заданную точку, то естественно начать вычислительный процесс следующим образом:
1)
для заданной точки ![]() вычисляем тангенс угла
наклона
вычисляем тангенс угла
наклона ![]() и движемся в этом направлении на
«небольшое» расстояние, выбираем следующую точку;
и движемся в этом направлении на
«небольшое» расстояние, выбираем следующую точку;
2) используя эту точку как начальную, повторяем процесс.
Этот удобный и простой метод тем не менее не лишен
ряда недостатков, например, для строго возрастающего решения задачи (1.1)
численное решение будет заметно меньше аналитического. Такой результат
определяется тем, что для получения следующей точки используется тангенс угла
наклона касательной в предыдущей точке. Чтобы избежать такой ошибки можно
изменить вычислительный процесс: сначала вычислить тангенс угла наклона
касательной в последующей точке, а затем продолжить движение в направлении
некоторой линейной комбинации начального и конечного тангенсов угла наклона.
Т.о. весь вычислительный алгоритм разбивается как бы на два этапа: 1) прогноз
(дальнейшего движения); 2) коррекция выбранного направления с учетом
предыдущего значения ![]() .
.
Методы прогноза и коррекции для интегрирования обыкновенных дифференциальных уравнений (ОДУ) широко используются благодаря следующим преимуществам:
1. Разность между прогнозируемым и скорректированным значениями дает оценку ошибок на каждом шаге вычислительного процесса и, следовательно, может быть использована для контроля величины шага интегрирования.
2. По сравнению с методами Рунге-Кутты на каждом шаге вычислительного процесса производная вычисляется реже.
Основные минусы методов прогноза и коррекции:
1. Неустойчивость.
2. Методы прогноза-коррекции не «самоначинающиеся» в отличие от методов Рунге-Кутты.
В паре прогноз-коррекция роль коррекции значительно важней, так как именно коррекция определяет общую устойчивость вычислительного процесса. Проанализируем способы построения прогнозов и коррекций на примере общих линейных формул, использующих информацию о функции и ее первой производной в последних трех точках.
Общий вид линейной трехточечной коррекции [1]:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.