Содержание работы. Пусть дано операторное уравнение:
, (2.18)
где
оператор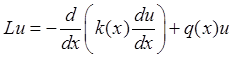 
- дифференциальный оператор, действующий в
Гильбертовом пространстве H. Метод Галеркина [5] основан на том, что невязка, т.е. разность между левой и
правой частью операторного уравнения 
в Гильбертовом
пространстве H равна нулю тогда и только тогда,
когда она ортогональна всем векторам любой полной системы. Поэтому для
определения приближенного решения уравнения (2.18) в заданном конечномерном
подпространстве пространства H достаточно
выписать условие ортогональности невязки всем базисным векторам этого
подпространства:
при этом не требуется самосопряженность оператора L.
Так как решение 
, то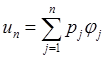 
, и
воспользовавшись свойствами скалярного произведения получим СЛАУ:
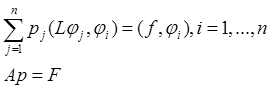, где
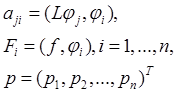
Выбирая в качестве базисных функций финитные функции [5] вида:
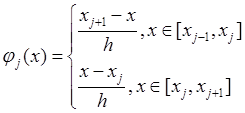
получим конечноэлементную аппроксимацию операторного уравнения (2.18). Если оператор L – самосопряженный, то метод Ритца [6] для заданной системы базисных функций дает такую же СЛАУ, что и метод Галеркина.
Варианты заданий.
1. Выполнить конечноэлементную аппроксимацию уравнения (2.8) с 1) первыми и третьими краевыми условиями и 2) вторыми и первыми краевыми условиями на линейных базисных функциях.
2. Выполнить конечноэлементную аппроксимацию уравнения (2.8) со 1) вторыми и третьими краевыми условиями и 2) третьими и третьими краевыми условиями на линейных базисных функциях.
3. Выполнить конечноэлементную аппроксимацию уравнения (2.8) с 1) первыми и третьими краевыми условиями и 2) вторыми и первыми краевыми условиями на квадратичных базисных функциях.
4. Выполнить конечноэлементную аппроксимацию уравнения (2.8) со 1) вторыми и третьими краевыми условиями и 2) третьими и третьими краевыми условиями на квадратичных базисных функциях.
5.
Выполнить конечноэлементную аппроксимацию нелинейного уравнения (2.8) 
с 1) первыми и третьими краевыми условиями
и 2) вторыми и первыми краевыми условиями на линейных базисных функциях.
6.
Выполнить конечноэлементную аппроксимацию нелинейного уравнения (2.8) со 1) вторыми и третьими краевыми
условиями и 2) третьими и третьими краевыми условиями на линейных базисных
функциях.
Оформление отчета.
Отчет по лабораторной работе должен включать следующие пункты.
1. Цель работы.
2. Содержание работы
2.1. Постановка задачи. Эквивалентная вариационная постановка.
Дискретный аналог задачи (2.8). Локальная матрица и локальный вектор правой части.
2.2. Алгоритм сборки глобальной матрицы СЛАУ и глобального вектора правой части. Метод решения СЛАУ.
2.3. Описание алгоритма решения краевой задачи.
2.4. Анализ результатов вычислительных
экспериментов. Результаты тестирования при постоянном коэффициенте
теплопроводности 
на вложенных сетках (не менее трех с шагом 
). Результаты тестирования с заданным коэффициентом
теплопроводности
на вложенных сетках. Результаты оформить в виде таблиц и графиков.
2.5. Выводы.
Список литературы.
1. Хемминг Р.В. Численные методы. - М.: Наука, 1972.
2. Деккер К., Вервер Я. Устойчивость методов Рунге-Кутты для жестких нелинейных дифференциальных уравнений. – М.: Мир, 1988.
3. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. - М.: Наука, 1985.
4. Самарский А.А. Введение в численные методы. - М.: Наука, 1987.
5. Лебедев В.И. Функциональный анализ и вычислительная математика. – М.: Физматлит, 2000.
6. Рояк М.Э., Соловейчик Ю.Г., Шурина Э.П. Сеточные методы решения краевых задач математической физики.: Учебное пособие. – Новосибирск.: Изд-во НГТУ, 1998.
7. Баландин М.Ю., Шурина Э.П. Методы решения СЛАУ большой размерности.: Учебное пособие. – Новосибирск.: Изд-во НГТУ, 2000.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.